题目内容
18.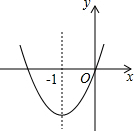 如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.
如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.
分析 根据函数的开口方向以及对称轴的位置即可判断a和b的符号,从而判断①,利用当x=1时函数值,结合图象判断②;求得函数与x轴的交点即可判断③.
解答 解:∵抛物线的开口向上,
∴a>0,
又∵对称轴在y轴的左侧,
∴b和a同号,即b>0,则ab>0,故①正确;
当x>0时,函数值大于0,则当x=1时,函数值是a+b+c>0,故②正确;
函数与x轴的一个交点是原点,对称轴是x=-1,则函数与x轴的另一交点是(-2,0).
则当-2<x<0时,y<0成立,故③正确.
故答案是:①②③.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
3.在不透明的袋中有一些除颜色外完全相同的白色和黑色棋子,从中随机取出一颗棋子是白色棋子的概率是$\frac{1}{4}$;若从盒中取出3颗黑色棋子后,再随机取出一颗棋子是白色棋子的概率为$\frac{2}{5}$,则盒中白色棋子有( )
| A. | 1颗 | B. | 2颗 | C. | 3颗 | D. | 4颗 |
7.计算2sin45°的结果等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.
已知在平面直角坐标系xOy中,点A(0,2),点B(1,0),现将线段BA绕点B按顺时针方向旋转90°得到线段BD,点C为线段AB的中点,连接CD.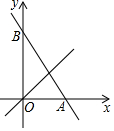 如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°.
如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°.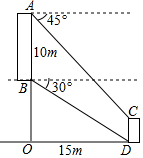 如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)
如图,从坡上建筑物AB观测坡底建筑物CD.从A点测得C点的俯角为45°,从B点测得D点的俯角为30°.已知AB的高度为10m,AB与CD的水平距离是OD=15m,则CD的高度为($5\sqrt{3}-5$)m(结果保留根号)