题目内容
17.已知a、b为两个连续整数,且a<$\sqrt{20}$-$\sqrt{5}$<b,则a+b=( )| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
分析 先估算出$\sqrt{20}$与$\sqrt{5}$的取值范围,再求出a,b的值,进而可得出结论.
解答 解:∵16<20<25,
∴4<$\sqrt{20}$<5.
∵4<5<9,
∴2<$\sqrt{5}$<3,
∴-3<-$\sqrt{5}$<-2,
∴4-3<$\sqrt{20}$-$\sqrt{5}$<5-2,即1<$\sqrt{20}$-$\sqrt{5}$<3,
∵a、b为两个整数,
∴a=2,b=3,
∴a+b=5.
故选:B.
点评 本题考查的是估算无理数的大小,熟知用有理数逼近无理数,求无理数的近似值是解答此题的关键.

练习册系列答案
相关题目
9.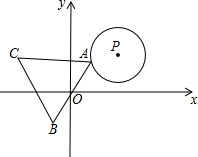 如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
 如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )
如图,⊙P在第一象限,半径为3.动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边三角形△ABC,点C在第二象限,点C随点A运动所形成的图形的面积为( )| A. | $\frac{{43\sqrt{3}}}{6}$ | B. | 27π | C. | $3\sqrt{3}π$ | D. | $\frac{{3\sqrt{3}}}{7}$π |
6.圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥的母线长为( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
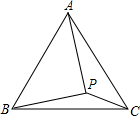 如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1.
如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1. 如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠D的度数是73°.
如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠D的度数是73°.
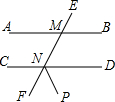 如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.
如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.