题目内容
2.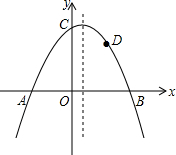 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标,若不存在,请说明理由.
分析 (1)由OA与OC的长确定出A与C的坐标,代入抛物线解析式求出b与c的值,即可确定出解析式;
(2)连接AD,与抛物线对称轴于点P,P为所求的点,设直线AD解析式为y=mx+n,把A与D坐标代入求出m与n的值,确定出直线AD解析式,求出抛物线对称轴确定出P横坐标,将P横坐标代入求出y的值,即可确定出P坐标.
解答  解:(1)∵OA=2,OC=3,
解:(1)∵OA=2,OC=3,
∴A(-2,0),C(0,3),
代入抛物线解析式得:$\left\{\begin{array}{l}{c=3}\\{-2-2b+3=0}\end{array}\right.$,
解得:b=$\frac{1}{2}$,c=3,
则抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3;
(2)连接AD,交对称轴于点P,则P为所求的点,
设直线AD解析式为y=mx+n(m≠0),
把A(-2,0),D(2,2)代入得:$\left\{\begin{array}{l}{-2m+n=0}\\{2m+n=2}\end{array}\right.$,
解得:m=$\frac{1}{2}$,n=1,
∴直线AD解析式为y=$\frac{1}{2}$x+1,
对称轴为直线x=$\frac{1}{2}$,
当x=$\frac{1}{2}$时,y=$\frac{5}{4}$,
则P坐标为($\frac{1}{2}$,$\frac{5}{4}$).
点评 此题考查了抛物线与x轴的交点,待定系数法求二次函数,一次函数解析式,以及对称轴-最短线路问题,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.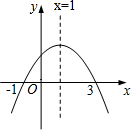 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )
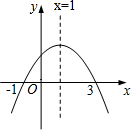 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③④ |
9.在下列图形中,①等边三角形,②正方形,③正五边形,④正六边形.其中既是轴对称图形又是中心对称的图形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,小花同学设计了一个圆直径的测量器,标有刻度的尺子在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,交圆E、F两点,读得刻度OE=8cm,OF=6cm,则圆的直径为10cm.
如图,小花同学设计了一个圆直径的测量器,标有刻度的尺子在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,交圆E、F两点,读得刻度OE=8cm,OF=6cm,则圆的直径为10cm. 在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),连结AD,作∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是( )
在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),连结AD,作∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.有下列结论:①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD=8;④3.6≤AE<10.其中正确的结论是( )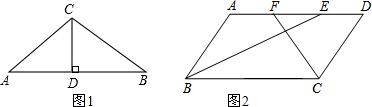
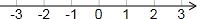 解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.
解不等式组$\left\{\begin{array}{l}x-1<2\\ 2x+9>3.\end{array}\right.$请结合题意填空,完成本小题的解答.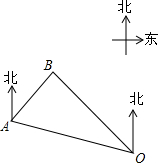 如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)