题目内容
6. 如图,抛物线与x轴交于A、B两点,与y轴交于点C,且点A的坐标为(-3,0),顶点D的坐标为(-1,4).
如图,抛物线与x轴交于A、B两点,与y轴交于点C,且点A的坐标为(-3,0),顶点D的坐标为(-1,4).(1)求该抛物线的表达式.
(2)求B、C两点的坐标.
(3)连接AD、AC、CD、BC,在y轴上是否存在点M,使得以M、B、C为顶点的三角形与△ACD相似?若存在,请求出点M的坐标;若不存在,请说明理由.
分析 (1)设抛物线的解析式为y=a(x+1)2+4,将点A的坐标代入可求得a的值,从而可得到抛物线的解析式;(2)将x=0代入求得对应的y值可得到点C的坐标,然后将y=0代入可求得对应的x的值可求得点B的坐标;
(3)由点A、B、C的坐标可求得,DC、AC、AD、BC的长,从而可得到∠DCA=90°,然后分为∠CMB=90°和∠CBM=90°两种情况求解即可.
解答 解:(1)设抛物线的解析式为y=a(x+1)2+4.
将点A的坐标为(-3,0)代入得:4a+4=0,解得:a=-1.
所以抛物线的表达式为y=-(x+1)2+4,y=-x2-2x+3.
(2)将x=0代入得:y=3,
∴C(0,3).
令y=0得:-x2-2x+3=0,解得:x=-3或x=1,
∴B(-1,0).
(3)∵A(3,0),C(0,3),D(-1,4),
∴DC=$\sqrt{2}$,AC=3$\sqrt{2}$,AD=2$\sqrt{5}$,BC=$\sqrt{10}$,
∴∠DCA=90°.
当∠CMB=90°时,点O与点M重合,
∴点M的坐标为(0,0).
当∠CBM=90°时,$\frac{CB}{CM}$=$\frac{AC}{AD}$,即$\frac{\sqrt{10}}{CM}$=$\frac{3\sqrt{2}}{2\sqrt{5}}$,解得:CM=$\frac{10}{3}$.
∴点M的坐标为(0,-$\frac{1}{3}$).
综上所述,点M的坐标为(0,0)或(0,-$\frac{1}{3}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,勾股定理的逆定理、相似三角形的性质,分类讨论是解题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
17.已知两个整数a,b,满足0<b<a<10,且$\frac{9a}{a+b}$是整数,那么数对(a,b)有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
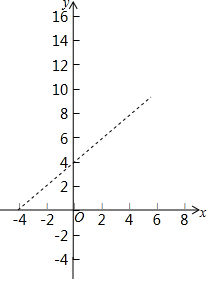 如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.
如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.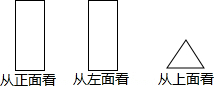 已知某几何体从正面和左面看都是大小相同的长方形,从上面看是一个等边三角形,如图所示.
已知某几何体从正面和左面看都是大小相同的长方形,从上面看是一个等边三角形,如图所示. 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.