题目内容
15.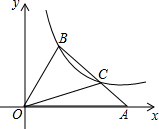 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设A的坐标是(a,0),设B的坐标是(m,n).则mn=k,C的坐标是($\frac{m+a}{2}$,$\frac{n}{2}$),然后根据C在反比例函数上,则$\frac{m+a}{2}$•$\frac{n}{2}$=k,再根据三角形的面积公式可得an=12,据此即可求解.
解答 解:设A的坐标是(a,0),设B的坐标是(m,n).则mn=k.
∵C是AB的中点,
∴C的坐标是($\frac{m+a}{2}$,$\frac{n}{2}$).
∵C在反比例函数上,
∴$\frac{m+a}{2}$•$\frac{n}{2}$=k,即(m+a)n=4k,mn+an=4k.
∵△OAB的面积是6,
∴$\frac{1}{2}$an=6,即an=12,
∴k+12=4k,
解得k=4.
故选B.
点评 本题考查了求反比例函数的解析式,正确设出未知数,转化为k的关系是关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
5.若m<n,下列不等式组无解的是( )
| A. | $\left\{\begin{array}{l}x>2m\\ x<2n\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<m-n\\ x<m+n\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>m\\ x>n-1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<m-2n\\ x>-n\end{array}\right.$ |
7.抛物线y=kx2-6x+9与x轴有两个交点,则k的取值范围( )
| A. | k<1且k≠0 | B. | k≠0 | C. | k<1 | D. | k>1 |
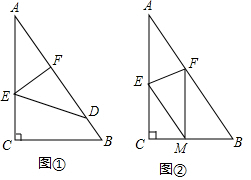
 如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=2,AB=6,则△ABD面积=6.
如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=2,AB=6,则△ABD面积=6. 如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD.
如图,己知∠1=∠2,要判定△ABD≌△ACD,则需要补充的一个条件为BD=CD.