题目内容
10. 如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=2,AB=6,则△ABD面积=6.
如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=2,AB=6,则△ABD面积=6.
分析 作DE⊥AB于E,根据角平分线的性质得到DE=DC=2,根据三角形的面积公式计算即可.
解答 解: 作DE⊥AB于E,
作DE⊥AB于E,
∵BD平分∠ABC,∠C=90°,DE⊥AB,
∴DE=DC=2,
∴△ABD面积=$\frac{1}{2}$×AB×DE=6,
故答案为:6.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
15.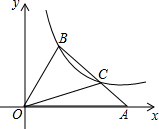 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
20. 如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )
如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )
 如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )
如图:已知直线y=x+1与坐标轴相交于点A,B;现把抛物线y=-x2的图象平移,使它的图象经过点A,B两点,则平移的方法是( )| A. | 向左平移一个单位 | B. | 向右平移一个单位 | ||
| C. | 向上平移一个单位 | D. | 向下平移一个单位 |
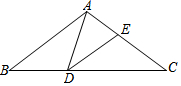 如图,在△ABC中,AB=AC=10,在BC边上取点D使BD=6,连结AD,以AD为一边作∠ADE=∠B交边AC于点E,如果sinB=$\frac{3}{5}$,则cos∠AED=$\frac{\sqrt{5}}{5}$.
如图,在△ABC中,AB=AC=10,在BC边上取点D使BD=6,连结AD,以AD为一边作∠ADE=∠B交边AC于点E,如果sinB=$\frac{3}{5}$,则cos∠AED=$\frac{\sqrt{5}}{5}$. (1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数.
(1)如图,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{7}{22}$∠AOE,求∠EOG和∠DOF的度数.