题目内容
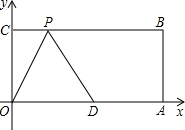 如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为
如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为考点:等腰三角形的判定,坐标与图形性质
专题:
分析:分OP=OD、PD=OD和PO=PD三种情况,结合矩形的性质和勾股定理可求得P点的坐标.
解答:解:
∵A(10,0),C(0,4),且四边形OABC是矩形,
∴OA=BC=10,OC=AB=4,
∵D是OA的中点,
∴OD=5,
当△ODP是腰长为5的等腰三角形时,则有PO=OD=5、PD=OD=5或PO=PD=5,
当PO=OD=5时,在Rt△OPC中,OC=4,OP=5,由勾股定理可求得PC=3,此时P点坐标为(3,4);
当PD=OD=5时,过P作PE⊥OA于点E,如图1,
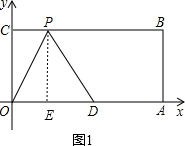
在Rt△PED中,PE=OC=4,PD=5,由勾股定理可求得DE=3,且OD=5,则OE=5-3=2,此时P点坐标为(2,4);
当PO=PD=5时,过P作PF⊥OA于点F,如图2,
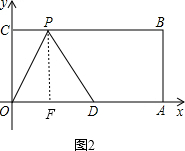
在Rt△POF中,PF=4,PO=5,由勾股定理可求得OF=3,则OD=6,与已知矛盾,故该情况不存在;
综上可知点P的坐标为(3,4)或(2,4),
故答案为:(3,4)或(2,4).
∵A(10,0),C(0,4),且四边形OABC是矩形,
∴OA=BC=10,OC=AB=4,
∵D是OA的中点,
∴OD=5,
当△ODP是腰长为5的等腰三角形时,则有PO=OD=5、PD=OD=5或PO=PD=5,
当PO=OD=5时,在Rt△OPC中,OC=4,OP=5,由勾股定理可求得PC=3,此时P点坐标为(3,4);
当PD=OD=5时,过P作PE⊥OA于点E,如图1,

在Rt△PED中,PE=OC=4,PD=5,由勾股定理可求得DE=3,且OD=5,则OE=5-3=2,此时P点坐标为(2,4);
当PO=PD=5时,过P作PF⊥OA于点F,如图2,

在Rt△POF中,PF=4,PO=5,由勾股定理可求得OF=3,则OD=6,与已知矛盾,故该情况不存在;
综上可知点P的坐标为(3,4)或(2,4),
故答案为:(3,4)或(2,4).
点评:本题主要考查等腰三角形的判定和性质及勾股定理,掌握等腰三角形的两腰相等分三种情况分别讨论求得P点的横坐标是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
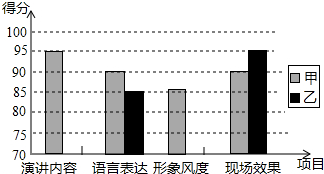 某校举办“社会主义核心价值观”知识演讲比赛,八(1)班计划从甲、乙两位同学中选出一位参加学校的决赛,已知这两位在预赛中各项成绩如表图,且甲、乙两人预赛四项成绩的平均分相同.
某校举办“社会主义核心价值观”知识演讲比赛,八(1)班计划从甲、乙两位同学中选出一位参加学校的决赛,已知这两位在预赛中各项成绩如表图,且甲、乙两人预赛四项成绩的平均分相同.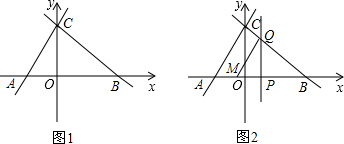
 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D. 如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB=
如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB= 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)经过A(-1,0)、B(3,0)两点,抛物线与y轴交点为C,其顶点为D,连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE. 如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值.
如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值.