题目内容
6.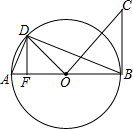 如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,(1)∠ADB=90°,理由是直径所对的圆周角是90°;
(2)若OA=$\sqrt{7}$,BC=3,求AD的长.
分析 (1)根据直径所对的圆周角是90°,即可得出;
(2)根据相似三角形的性质推出$\frac{AD}{OB}=\frac{AB}{OC}$,代入求出即可.
解答 解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,理由是直径所对的圆周角是90°,
故答案为:90°,直径所对的圆周角是90°;
(2)OB=OA=$\sqrt{7}$,
在△OBC中,由勾股定理得:OC=$\sqrt{O{B}^{2}+B{C}^{2}}=\sqrt{7+9}=4$,
∵△ADB∽△OBC,
∴$\frac{AD}{OB}=\frac{AB}{OC}$,
∴$\frac{AD}{\sqrt{7}}=\frac{2\sqrt{7}}{4}$,
解得:AD=3.5.
答:AD的长是3.5.
点评 本题考查了切线的性质,勾股定理,相似三角形的性质和判定,圆周角定理等知识点得出应用,关键是求出△ADB∽△OBC,此题是一道比较典型的题目.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
16.有一个从袋子中摸球的游戏,小红根据游戏规则,作出了如图所示的树形图,则此次摸球的游戏规则是( )
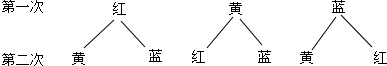
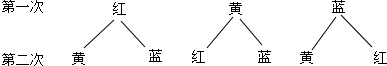
| A. | 随机摸出一个球后放回,再随机摸出1个球 | |
| B. | 随机摸出一个球后不放回,再随机摸出1个球 | |
| C. | 随机摸出一个球后放回,再随机摸出3个球 | |
| D. | 随机摸出一个球后不放回,再随机摸出3个球 |
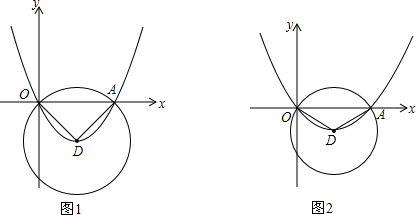
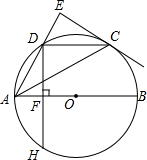 如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC.
如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC.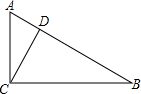 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8.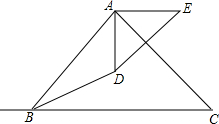 如图,已知AB⊥AC,DA⊥AE,AB=AC,AD=AE,求证:BD=CE.
如图,已知AB⊥AC,DA⊥AE,AB=AC,AD=AE,求证:BD=CE.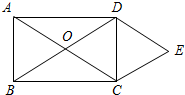 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.