题目内容
11.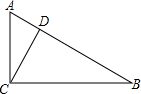 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=8.
分析 先根据相似三角形判定得到△ACD~△ABC,再根据相似三角形的性质得到等积式,求出AB,由勾股定理即可求出结论.
解答 解:∵∠ACD=∠B,∠CAD=∠BAC,
∴△ACD~△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AB•AD,
∵AC=6,AD=3.6,
∴AB=10,
在RtABC中,
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8.
故答案为8.
点评 本题主要考查了相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质是解决问题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
5.-$\frac{1}{5}$的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | -5 |
3.sin45°的值等于( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
1.-$\frac{2}{3}$的相反数是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
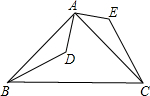 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连结BD、CE.求证:BD=CE.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连结BD、CE.求证:BD=CE.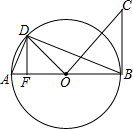 如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,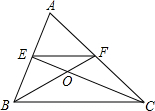 如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )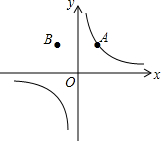 如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.
如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.