Question

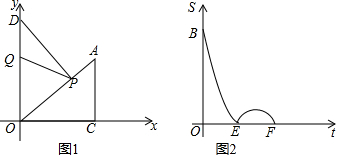
2．Rt△AOB在直角坐标系中的位置如图，已知OA=2，OB=4，现在Rt△AOB剪裁一个矩形DEOF，要求D、E、F分别在AB、BO、AO上，怎样剪裁面积最大，最大面积为多少？

Answer 1

分析 设OF=x，根据矩形的性质得到DE=OF=x，根据相似三角形的性质得到OE=4-2x，根据矩形的面积公式得到S=-2（x-1）²+2，即可得到结论．

解答 解：设OF=x，
∵四边形DEOF是矩形，
∴DE=OF=x，
∵DE∥OA，
∴△BDE∽△BAO，
∴$\frac{DE}{OA}=\frac{BE}{OB}$，
∴OE=4-2x，
设矩形DEOF的面积=S，
∴S=DE•OE=x•（4-2x）=-2x²+4x，
即S=-2（x-1）²+2，
∴当OF=1时，S_最大=2．

点评 本题考查了相似三角形的判定和性质，二次函数的最值问题，矩形的性质与锐角的正切的利用，（2）把二次函数的解析式转互为顶点式形式是解题的关键．