题目内容
7. 在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )
在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,则∠A的度数为( )| A. | 80度 | B. | 50度 | C. | 100度 | D. | 110度 |
分析 先根据角平分线的定义得到∠ABC=2∠1,∠ACB=2∠2,求得∠ABC+∠ACB,最后再根据三角形内角和定理得∠A+∠ABC+∠ACB=180°,据此求得∠A的度数即可.
解答  解:∵BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,
解:∵BO,CO分别平分∠ABC和∠ACB,∠1+∠2=50°,
∴∠ABC=2∠1,∠ACB=2∠2,
∴∠ABC+∠ACB=2(∠1+∠2)=100°,
∵△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠A=180°-100°=80°.
故选:A.
点评 本题主要考查了角平分线的定义以及三角形内角和定理,解题时注意运用三角形内角和是180°.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
8. 如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
 如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )
如图,在△ABC中,∠ACB=120°,AC=AE,BC=BD,则∠DCE的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
 Rt△AOB在直角坐标系中的位置如图,已知OA=2,OB=4,现在Rt△AOB剪裁一个矩形DEOF,要求D、E、F分别在AB、BO、AO上,怎样剪裁面积最大,最大面积为多少?
Rt△AOB在直角坐标系中的位置如图,已知OA=2,OB=4,现在Rt△AOB剪裁一个矩形DEOF,要求D、E、F分别在AB、BO、AO上,怎样剪裁面积最大,最大面积为多少?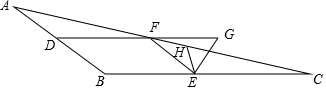 如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.
如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.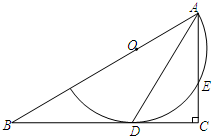 在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AB于点E,连接AD.
在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AB于点E,连接AD.