题目内容
8.如图,在平面直角坐标系中,已知点A(0,4),△AOB为等边三角形,M是x轴负半轴上的一个动点(不与原点O重合),以线段AM为一边在其右侧作等边三角形△AMN.(1)求点B的坐标;
(2)在点M运动过程中,∠ABN的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接ON,当ON∥AB时,求M的坐标.

分析 (1)作BH⊥x轴于H,根据等边三角形的性质求出∠BOH=30°,解直角三角形求出BH、OH,得到点B的坐标;
(2)证明△MAO≌△NAB,根据全等三角形的性质得到∠ABN=∠AOM=90°;
(3)作NH⊥x轴于H,根据直角三角形的性质、勾股定理计算即可.
解答 解:(1) 作BH⊥x轴于H,
作BH⊥x轴于H,
∵△AOB是等边三角形,
∴∠BOH=30°,
∴BH=$\frac{1}{2}$OB=2,OH=OB×cos30°=2$\sqrt{3}$,
∴点B的坐标为(2$\sqrt{3}$,3);
(2)∠ABN=90°,则∠ABN的大小不变,
∵△AOB、△AMN为等边三角形,
∴∠MAO=∠NAB,
在△MAO和△NAB中,
$\left\{\begin{array}{l}{AM=AN}\\{∠MAO=∠NAB}\\{AO=BO}\end{array}\right.$,
∴△MAO≌△NAB,
∴∠ABN=∠AOM=90°,
则∠ABN=90°,则∠ABN的大小不变;
(3)作NH⊥x轴于H,
∵ON∥AB,
∴∠ONB=∠ABN=90°,
∵∠ABN=90°,∠ABO=60°,
∴∠OBN=30°,
∴ON=$\frac{1}{2}$OB=2,BN=2$\sqrt{3}$,
∴AN=$\sqrt{A{B}^{2}+B{N}^{2}}$=2$\sqrt{7}$,
∴MN=AN=$\sqrt{7}$,
∵∠HON=30°,
NH=$\frac{1}{2}$ON=1,OH=$\sqrt{3}$,
∴MH=$\sqrt{M{N}^{2}-N{H}^{2}}$=3$\sqrt{3}$,
∴OM=2$\sqrt{3}$,
∴M的坐标为(-2$\sqrt{3}$,0).
点评 本题考查的是等边三角形的性质、全等三角形的判定和性质以及直角三角形的性质,掌握相关的判定定理和性质定理是解题的关键.

| A. | $\frac{1}{2017}$ | B. | 2016 | C. | 2017 | D. | 2018 |
| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 12cm2 |
| 摸球的次数S | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率 | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{3}$×$\sqrt{4}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | (-$\sqrt{3}$)2=-3 |


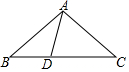 如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.
如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.