题目内容
20.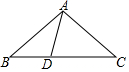 如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.
如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.
分析 首先过A作AE⊥BC,当D与E重合时,AD最短,首先利用等腰三角形的性质可得BE=EC,进而可得BE的长,利用勾股定理计算出AE长,然后可得AD的取值范围,进而可得答案.
解答  解:过A作AE⊥BC,
解:过A作AE⊥BC,
∵AB=AC,
∴EC=BE=$\frac{1}{2}$BC=4,
∴AE=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵D是线段BC上的动点(不含端点B、C).
∴3≤AD<5,
∴AD=3或4,
∵线段AD长为正整数,
∴AD的可以有三条,长为4,3,4,
∴点D的个数共有3个,
故答案为:3.
点评 此题主要考查了等腰三角形的性质和勾股定理,关键是正确利用勾股定理计算出AD的最小值,然后求出AD的取值范围.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
10.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.从一只船上看一小岛,方向为北偏东35°,从小岛上看这只船,其方向为( )
| A. | 南偏西35° | B. | 南偏东55° | C. | 北偏东55° | D. | 北偏西35° |
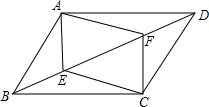 如图,在?ABCD中,已知点E、F在对角线边BD上,且BE=DF,求证:四边形AECF是平行四边形.
如图,在?ABCD中,已知点E、F在对角线边BD上,且BE=DF,求证:四边形AECF是平行四边形.