题目内容
15. 如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点.
如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点.(1)a=-$\frac{2}{3}$,b=$\frac{4}{3}$;
(2)若点D为线段OB上一点,连接AD,作AC⊥AD交y轴正半轴于点C.
①当点D坐标为($\frac{2}{3}$,0)时,AC经过y=ax2+bx+2的顶点P;
②连结CD、AB,设△ADC与△ABD的面积之差为S,问:当点D在何处时S最小,并求出这个最小值.
分析 (1)把A、B坐标代入可求得答案;
(2)①设抛物线与y轴交于点E,连接AE,过A作AF⊥x轴于点F,由条件可证明△AEC≌△AFD,则可求得D点坐标;②
解答 解:
(1)∵抛物线y=ax2+bx+2经过A,B两点,
∴$\left\{\begin{array}{l}{4a+2b+2=2}\\{9a+3b+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
故答案为:-$\frac{2}{3}$;$\frac{4}{3}$;
(2)①由(1)知,经过A、B、P的抛物线为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2,故顶点P的坐标为(1,$\frac{8}{3}$).
如图1,设抛物线与y轴交于点E,连接AE,则AE∥x轴,过点A作AF⊥x于点F,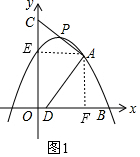
则AE=AF=2,
∵∠CAD=∠EAF=90°,
∴∠CAE=∠FAD
在△ACE与△ADF中
$\left\{\begin{array}{l}{∠CAE=∠FAD}\\{∠CEA=∠AFD=90°}\\{AE=AF}\end{array}\right.$
∴△ACE≌△ADF(AAS).
∴CE=DF,
设直线AP解析式为y=kx+s,
∴$\left\{\begin{array}{l}{2k+s=2}\\{k+s=\frac{8}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{s=\frac{10}{3}}\end{array}\right.$,
∴直线AP解析式为y=-$\frac{2}{3}$x+$\frac{10}{3}$,令x=0可得y=$\frac{10}{3}$,
∴OC=$\frac{10}{3}$,且OE=2,
∴DF=CE=$\frac{10}{3}$-2=$\frac{4}{3}$,
∵F(2,0),
∴OF=2,
∴OD=OF-DF=2-$\frac{4}{3}$=$\frac{2}{3}$,
∴D($\frac{2}{3}$,0),
故答案为:($\frac{2}{3}$,0);
②设BD=a,则FD=a-1,
∴AD2=DF2+AF2=(a-1)2+22=a2-2a+5,
又AC=AD,
∴S△ACD=$\frac{1}{2}$AC•AD=$\frac{1}{2}$(a2-2a+5),
又∵S△ADB=$\frac{1}{2}$DC•AD=$\frac{1}{2}$×a×2=a,
∴S=$\frac{1}{2}$(a2-2a+5)-a=$\frac{1}{2}$a2-2a+$\frac{5}{2}$,
即S=$\frac{1}{2}$(a-2)2+$\frac{1}{2}$;
∴当a=2(在0<a<3范围内)时,S最小值=$\frac{1}{2}$,
即当点D在(1,0)时,S最小值为$\frac{1}{2}$.
点评 本题主要考查了二次函数解析式的确定、全等三角形的判定和性质以及三角形面积的求法等重要知识点,能够正确的将求图形面积最大(小)问题转换为二次函数求最值的问题是解答(2)②题的关键.

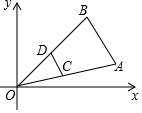 如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(8,2),B (6,6),以原点O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段CD,则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,1) | D. | (4,1) |
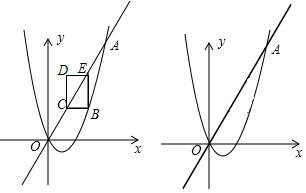
 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.