题目内容
7. 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE,试说明BE与AD的数量与位置关系.
分析 根据已知条件证明△ACD≌△BCE(SAS);然后由全等三角形的性质:对应边与对应角相等求得AD=BE,∠EBC=∠DAC,由角的互余关系即可得出AD⊥BE.
解答 解:AD=BE,且AD⊥BE.理由如下:如图,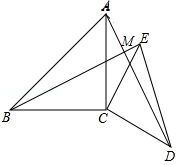
∵AC=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠A=∠ABC=∠CBE=∠CEB=45°;∠ACD=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACD=∠BCE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
∴AD=BE(全等三角形的对应边相等),
∴∠EBC=∠DAC(全等三角形的对应角相等),
∵∠BMD=∠ABE+∠BAC+∠CAD=∠ABE+∠EBC+∠BAC=45°+45°=90°,
∴AD⊥BE.
点评 本题考查了全等三角形的判定与性质.解答AD⊥BE的关键是利用等腰直角三角形的性质求得∠EBC=∠DAC=45°.

练习册系列答案
相关题目
18.下列运算结果正确的是( )
| A. | 5a-3a=2 | B. | -2x2y+3xy2=x2y | ||
| C. | 4x2-3x=x | D. | -6a2b-6a2b=-12a2b |
5.下列条件是随机事件的是( )
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 在只装有黑球和白球的袋子里,摸出红球 | |
| C. | 购买一张彩票,中奖 | |
| D. | 太阳从东方升起 |
 如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点.
如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点. 分别在如图的圆圈内填入不同的整数,使得每条线上的3个数之和都为0,至少写出三种答案.
分别在如图的圆圈内填入不同的整数,使得每条线上的3个数之和都为0,至少写出三种答案. 如图,在△ABC中,AB=6cm,BC=12cm,动点P从A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三点连成的三角形与△ABC相似.
如图,在△ABC中,AB=6cm,BC=12cm,动点P从A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;t=$\frac{3}{2}$s或$\frac{3}{5}$s,由P、B、Q三点连成的三角形与△ABC相似. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、