题目内容
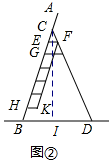
13.如图①,小华家阳台上放置了一个有6级踏板的人字梯,如图②是人字梯的侧面示意图,梯梁AB与CD相交于点C,现将人字梯完全稳固张开,B,D两点立于水平地面,从下至上,HK是第1级,EF是第6级,每级踏板均与水平地面平行,相邻两级踏板间的距离相等,最上面的踏板EF恰好横于AB,CD之间,经测量:AB=2m,CD=1.75m,EF=0.2m,AC=CE=EG=HB=CF=0.25m.(1)求人字梯完全稳固张开时,梯子下端B,D间的距离;
(2)求梯梁AB与最上面踏板EF的夹角∠CEF的度数;
(3)小华家天花板距离地面3m,小华静止站立时伸直手臂摸到的最大高度为2m,那么,小华要摸到天花板,至少要站在人字梯的第几级踏板上?(参考数据:sin66.4°≈0.92,cos66.4°≈0.4,tan23.6°≈0.44)

分析 (1)由题意可知:EF∥BD,所以△CEF∽△CBD,利用对应边的比相等即可求出BD的值.
(2)过点C作CI⊥BD于I点,由于CB=CD,所以点I是BD的中点,利用cos∠CBI的值即可求出∠CEF的度数.
(3)假设MN是小华,且MN=2,NJ是天花板,且IJ=3,过点M作MP⊥BD于点P,利用sin∠CBI=$\frac{MP}{BM}$求出BM的长度,然后即可求出需要站在第几级上.
解答 解:(1)∵AB=2,AC=0.25,
∴CB=AB-AC=1.75
∵EF∥BD
∴△CEF∽△CBD
∴$\frac{CE}{CB}=\frac{EF}{BD}$
∴BD=1.4m
(2) 过点C作CI⊥BD于I点,
过点C作CI⊥BD于I点,
∵CB=CD=1.75,
∴△CBD是等腰三角形.
∴BI=$\frac{1}{2}$BD=0.7
∴cos∠CBI=$\frac{BI}{CB}$=0.4
∴∠CBI≈66.4°,
∵EF∥BD
∴∠CEF=∠CBD=66.4°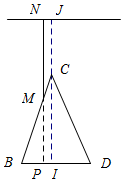
(3)假设MN是小华,且MN=2,
NJ是天花板,且IJ=3,
过点M作MP⊥BD于点P,
∴MP=NP-MN=3-2=1,
∴sin∠CBI=$\frac{MP}{BM}$,
∴BM=$\frac{MP}{sin66.4°}$≈1.086,
由于相邻两级踏板间的距离相等,且BH=0.25
∴1.086÷0.25≈4.34
故小华要摸到天花板,至少要站在人字梯的第5级踏板上
点评 本题考查解直角三角形的应用,涉及等腰三角形的性质,相似三角形的判定与性质,锐角三角函数等知识.

练习册系列答案
相关题目
8.实数1,-1,0,-$\frac{1}{2}$四个数中,最大的数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | $-\frac{1}{2}$ |
5.下列条件是随机事件的是( )
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 在只装有黑球和白球的袋子里,摸出红球 | |
| C. | 购买一张彩票,中奖 | |
| D. | 太阳从东方升起 |
2.某市2016年10月份某日的一天的温差为9℃,最高温度为t℃,则最低气温可表示为( )
| A. | (t-9)℃ | B. | (9-t)℃ | C. | (-9-t)℃ | D. | (t+9)℃ |
3.-$\frac{1}{6}$的倒数是( )
| A. | 6 | B. | $\frac{1}{6}$ | C. | -6 | D. | -$\frac{1}{6}$ |
 如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点.
如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.