题目内容
6.如图,已知抛物线y=$\frac{1}{2}$x2+bx与直线y=2x交于点O(0,0),A(a,12).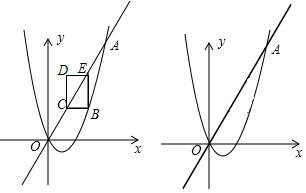
(1)求抛物线的解析式.
(2)点B是抛物线上O、A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C、E,以BE、BC为边构造矩形BCDE,设点D的坐标为(m,n),求m,n之间的关系式.
(3)将射线OA绕原点逆时针旋转45°后与抛物线交于点P,求P点的坐标.
分析 (1)把点A的坐标代入一次函数解析式求得a的值;然后把点A的坐标代入二次函数解析式来求b的值即可;
(2)根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式;
(3)如图2,作∠POA=45°,交抛物线与P,过P作PQ⊥OA于Q,过P作PM⊥x轴于M,过Q作QN⊥PM于N交y轴于R,构建全等三角形△PNQ≌△QRO,结合全等三角形的对应边相等和二次函数图象上点的坐标特征来求点P的坐标.
解答 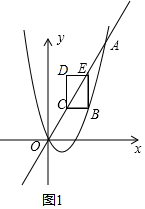 解:(1)∵点A(a,12)在直线y=2x上,
解:(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,
又∵点A是抛物线y=$\frac{1}{2}$x2+bx上的一点,
将点A(6,12)代入y=$\frac{1}{2}$x2+bx,可得b=-1,
∴抛物线解析式为y=$\frac{1}{2}$x2-x;
(2)如图1,∵直线OA的解析式为:y=2x,点D的坐标为(m,n),
∴点E的坐标为($\frac{1}{2}$n,n),点C的坐标为(m,2m),
∴点B的坐标为($\frac{1}{2}$n,2m),
把点B($\frac{1}{2}$n,2m)代入y=$\frac{1}{2}$x2-x,可得m=$\frac{1}{16}$n2-$\frac{1}{4}$n,
∴m、n之间的关系式为m=$\frac{1}{16}$n2-$\frac{1}{4}$n;
(3)如图2,作∠POA=45°,交抛物线与P,过P作PQ⊥OA于Q,过P作PM⊥x轴于M,过Q作QN⊥PM于N交y轴于R,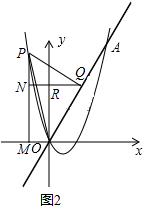
则△PNQ≌△QRO,
所以NQ=RO,PN=QR,
设Q点为(t,2t),则P为(-t,3t),代入抛物线解析式得$\frac{1}{2}$t2+t=3t,
解得:t1=0,t2=4,
∵t>0,
∴P点的坐标为(-4,12).
点评 本题考查了二次函数综合题,需要掌握矩形的性质、待定系数法求二次函数解析式的知识,解答本题需要同学们能理解矩形四个顶点的坐标之间的关系.

 阅读快车系列答案
阅读快车系列答案| A. | 5a-3a=2 | B. | -2x2y+3xy2=x2y | ||
| C. | 4x2-3x=x | D. | -6a2b-6a2b=-12a2b |
 已知:∠AOB,点M、N.求作:点P,使点P在∠AOB的平分线上,且PM=PN.(要求:用尺规作图,保留作图痕迹,不写作法).
已知:∠AOB,点M、N.求作:点P,使点P在∠AOB的平分线上,且PM=PN.(要求:用尺规作图,保留作图痕迹,不写作法).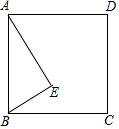 如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF. 如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点.
如图,在平面直角坐标系中,A(2,2),B(3,0),抛物线y=ax2+bx+2经过A,B两点. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(1,0)、