题目内容
8.如图l,△ACB和△DCE均为等边三角形,点D在AC边上,现将△DCE绕点C逆时针旋转.问题发现:当点A、D、E在同一直线上时,连接BE,如图2,
〔1)求证:△ACD≌△BCE;
〔2)求证:CD∥BE.
拓展探究
如图1,若CA=2$\sqrt{3}$,CD=2,将△DCE绕点C按逆对针方向旋转,旋转角度为α(0°<α<360°),如图3,α为90°或270°时,△CAD的面积最大,最大面积是$2\sqrt{3}$.
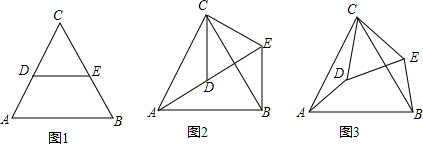
分析 问题发现:(1)由△ACB和△DCE为等边三角形知AC=BC、CD=CE、∠ACB=∠DCE=60°,从而可得∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE.即可证得△ACD≌△BCE.
(2)由△ACD≌△BCE知∠ADC=∠BEC,根据∠EDC=60°知∠ADC=∠BEC=120°,由∠DCE+∠CEB=60°+120°=180°可证得CD∥BE.
拓展探究:作DF⊥AC于点F,由S△ACD=$\frac{1}{2}$AC•DF=$\sqrt{3}$DF知DF取得最大值时△CAD面积最大,由△CFD中,DF<CD知只有当CD旋转到与AC垂直时,FD才能取得最大值,即FD=CD,由于旋转角0°<α<360°,所以除了旋转90°以外,旋转270°也满足条件,继而可得最大面积.
解答 解:问题发现:
(1)∵△ACB和△DCE为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(2)∵△ACD≌△BCE,
∴∠ADC=∠BEC,
又∵∠EDC=60°,
∴∠ADC=∠BEC=120°,
∴∠DCE+∠CEB=60°+120°=180°,
∴CD∥BE(内错角互补两直线平行);
拓展探究:
如图,过点D作DF⊥AC于点F,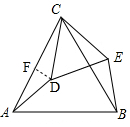
∵S△ACD=$\frac{1}{2}$AC•DF=$\sqrt{3}$DF,
∴当DF取得最大值时△CAD面积最大,
又∵在△CFD中,DF<CD,
∴只有当CD旋转到与AC垂直时,FD才能取得最大值,即FD=CD=2,
∵旋转角度为0°<α<360°,
∴当α=90°或270°时,△CAD的面积最大,最大面积是2$\sqrt{3}$,
故答案为:90°或270°,2$\sqrt{3}$.
点评 本题主要考查全等三角形的判定与性质、旋转的性质、平行线的判定等知识点,熟练掌握旋转的性质是解题的关键

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 在△ABC中,点D为BC上一点,连接AD,点E在BD上,且DE=CD,过点E作AB的平行线交AD于F,且EF=AC.如图,求证:∠BAD=∠CAD.
在△ABC中,点D为BC上一点,连接AD,点E在BD上,且DE=CD,过点E作AB的平行线交AD于F,且EF=AC.如图,求证:∠BAD=∠CAD.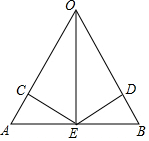 在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.
在△OAB中,E是AB的中点,且EC、ED分别垂直OA,OB,垂足为C、D,AC=BD,求证:OE是∠AOB的角平分线.