Question

4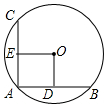．如图，在⊙O中，相等的弦AB、AC互相垂直，OE⊥AC于E，OD⊥AB于D，则四边形OEAD为（　　）

• A． 正方形
• B． 菱形
• C． 矩形
• D． 平行四边形

Answer 1

分析 先根据垂径定理，由OD⊥AB，OE⊥AC得到AD=$\frac{1}{2}$AB，AE=$\frac{1}{2}$AC，且∠ADO=∠AEO=90°，加上∠DAE=90°，则可判断四边形ADOE是矩形，由于AB=AC，所以AD=AE，于是可判断四边形ADOE是正方形．

解答 证明：∵OD⊥AB于D，OE⊥AC于E，
∵AD=$\frac{1}{2}$AB，AE=$\frac{1}{2}$AC，∠ADO=∠AEO=90°，
∵AB⊥AC，
∴∠DAE=90°，
∴四边形ADOE是矩形，
∵AB=AC，
∴AD=AE，
∴四边形ADOE是正方形；
故选A．

点评 本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了正方形的判定．