题目内容
2.计算:(1)$\frac{{m}^{2}}{m-n}$+$\frac{{n}^{2}}{n-m}$
(2)($\frac{{x}^{2}-4x+4}{{x}^{2}-4}$-$\frac{x}{x+2}$)÷$\frac{x-1}{x+2}$.
分析 根据分式的运算法则即可求出答案
解答 解:(1)原式=$\frac{{m}^{2}-{n}^{2}}{m-n}$=m+n
(2)原式=($\frac{(x-2)^{2}}{{x}^{2}-4}$-$\frac{x}{x+2}$)÷$\frac{x-1}{x+2}$
=($\frac{x-2}{x+2}$-$\frac{x}{x+2}$)×$\frac{x+2}{x-1}$
=$\frac{-2}{x+2}$×$\frac{x+2}{x-1}$
=$-\frac{2}{x-1}$
点评 本题考查分式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
12.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(不需化简):
(2)如果批发商希望通过销售这批T恤获利8960元,那么第二个月的单价应是多少?
(3)批发商通过销售这批T恤有没有可能获利10000元,为什么?
(1)填表(不需化简):
| 时间 | 第一个月 | 第二个月 | 清仓时 | |
| 单价(元) | 80 | 80-x | 40 | |
| 销售量(件) | 200 | 200+10x | 400-10x |
(3)批发商通过销售这批T恤有没有可能获利10000元,为什么?
 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.
如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.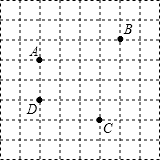 如图,已知A、B、C、D是网格纸上的四个格点,根据要求在网格中画图.
如图,已知A、B、C、D是网格纸上的四个格点,根据要求在网格中画图.