题目内容
10. △ABC内接于⊙O,AD平分∠BAC交⊙O于点D,DE∥AB交⊙O于E,交AC于P.求证:AC=DE;PO平分∠APD.
△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,DE∥AB交⊙O于E,交AC于P.求证:AC=DE;PO平分∠APD.
分析 作OM⊥AC于M,ON⊥DE于N,如图,由角平分线定义得到∠1=∠2,再由平行线性质得∠D=∠1,则∠2=∠D,于是根据圆周角定理得$\widehat{CD}$=$\widehat{AE}$,所以$\widehat{DE}$=$\widehat{AC}$,则根据圆心角、弧、弦的关系得到AC=DE,所以OM=ON,然后根据角平分线的性质定理的逆定理得到PO平分∠APD.
解答 证明:作OM⊥AC于M,ON⊥DE于N,如图,
∵AD平分∠BAC,
∴∠1=∠2,
∵DE∥AB,
∴∠D=∠1,
∴∠2=∠D,
∴$\widehat{CD}$=$\widehat{AE}$,
∴$\widehat{CD}$+$\widehat{CE}$=$\widehat{AE}$+$\widehat{CE}$,即$\widehat{DE}$=$\widehat{AC}$,
∴AC=DE,
∴OM=ON,
而OM⊥AC于M,ON⊥DE于N
∴PO平分∠APD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两条的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理和角平分线的性质定理的逆定理.

练习册系列答案
相关题目
20.“十一”黄金周,某商场举办促销活动,下表为为该商场当天与前一天的营业额相比较的涨跌情况.已知9月30日的营业额为26万元.
(1)黄金周内收入最高的是10月4日,最低的是10月7日;
(2)黄金周内平均每天的营业额是多少?
| 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 4 | 3 | 1 | 1 | -4 | -3 | -2 |
(2)黄金周内平均每天的营业额是多少?
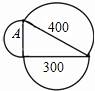 如图,半圆内数字分别为所在半圆的面积,则图中字母A所代表的半圆面积是100.
如图,半圆内数字分别为所在半圆的面积,则图中字母A所代表的半圆面积是100.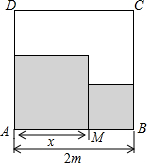 如图,在边长为2m的正方形铁板内,沿着一条边恰好截取两块相邻的正方形板料,要使截取的板料面积最小,应该怎样截取?
如图,在边长为2m的正方形铁板内,沿着一条边恰好截取两块相邻的正方形板料,要使截取的板料面积最小,应该怎样截取?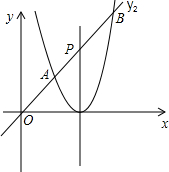 将抛物线y1=2x2向右平移2个单位长度,得到抛物线y2的图象,如图所示.
将抛物线y1=2x2向右平移2个单位长度,得到抛物线y2的图象,如图所示. 如图,将一根25cm长的细木棒放入长、宽、高的平方分别为64cm2、36cm2和300cm2的长方体无盖盒子中,则细木棒露在盒外面的最短长度是5cm.
如图,将一根25cm长的细木棒放入长、宽、高的平方分别为64cm2、36cm2和300cm2的长方体无盖盒子中,则细木棒露在盒外面的最短长度是5cm.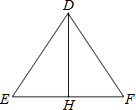 如图,在△DEF中,DE=DF=10,点H在EF上,DH=8,EH=6,请说明:DH平分∠EDF?
如图,在△DEF中,DE=DF=10,点H在EF上,DH=8,EH=6,请说明:DH平分∠EDF?