Question

1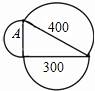．如图，半圆内数字分别为所在半圆的面积，则图中字母A所代表的半圆面积是100．

Answer 1

分析 由于正方形的面积等于边长的平方，根据勾股定理求出面积是A的半圆的直径的平方，进而即可求得半圆的面积A．

解答 解：∵以EG为直径的半圆的面积等于400，即$\frac{1}{2}$π（$\frac{EG}{2}$）²=400，
∴EG²=$\frac{3200}{π}$，
∵以FG为直径的半圆的面积为300，
∴$\frac{1}{2}$π（$\frac{FG}{2}$^）2=300，
∴FG²=$\frac{2400}{π}$，
又∵△EFG为直角三角形，根据勾股定理得：
EG²=EF²+FG²，
∴EF²=EG²-FG²=$\frac{800}{π}$，
则半圆的面积为：A=$\frac{1}{2}$π（$\frac{EF}{2}$）²=$\frac{1}{2}$π×$\frac{1}{4}$•EF²=100．
故答案为100．

点评 此题考查了圆的面积公式以及勾股定理，熟记圆的面积和勾股定理是解题的关键．