题目内容
2．
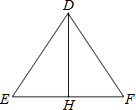如图，在△DEF中，DE=DF=10，点H在EF上，DH=8，EH=6，请说明：DH平分∠EDF？
分析 先由勾股定理的逆定理得出∠DHE=90°，即DH⊥EF，又DE=DF，根据等腰三角形三线合一的性质即可证明DH平分∠EDF．
解答 证明：∵DE=10，DH=8，EH=6，
∴62+82=102，即DH2+EH2=DE2，
∴△DEH是直角三角形，∠DHE=90°，即DH⊥EF，
又∵DE=DF，
∴DH平分∠EDF．
点评 本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．也考查了等腰三角形三线合一的性质．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
△ABC内接于⊙O，AD平分∠BAC交⊙O于点D，DE∥AB交⊙O于E，交AC于P．求证：AC=DE；PO平分∠APD．
17．要使代数式$\sqrt{2x+3}$有意义，字母x必须满足的条件是（ ）
| A． | x＞$\frac{3}{2}$ | B． | x≥$\frac{3}{2}$ | C． | x＞-$\frac{3}{2}$ | D． | x≥-$\frac{3}{2}$ |
11．已知关于x的一元二次方程x2-2x=m有两个不相等的实数根，则m的取值范围是（ ）
| A． | m＜1 | B． | m＜-2 | C． | m=0 | D． | m＞-1 |