Question

5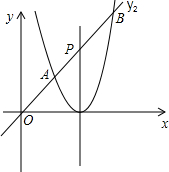．将抛物线y₁=2x²向右平移2个单位长度，得到抛物线y₂的图象，如图所示．
（1）求y₂的函数表达式；
（2）设抛物线的对称轴交直线y=x于点P，求点P的坐标；
（3）设直线y=x与抛物线交于A，B两点，求A，B两点的坐标．

Answer 1

分析 （1）根据“左加右减”的法则进行变换即可得到抛物线y₂的表达式．
（2）把x=2代入y=x，求得y=2，从而求得P（2，2）；
（3）联立方程，解方程即可求得．

解答 解：（1）由题意得：y₂=2（x-2）²=2x²-8x+8．
（2）∵对称轴为直线x=2，
把x=2代入y=x得y=2，
∴P（2，2）；
（3）解$\left\{\begin{array}{l}{y=x}\\{y=2（x-2）^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{9+\sqrt{15}}{4}}\\{y=\frac{9+\sqrt{15}}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{9-\sqrt{15}}{4}}\\{y=\frac{9-\sqrt{15}}{4}}\end{array}\right.$，
∴A（$\frac{9-\sqrt{15}}{4}$，$\frac{9-\sqrt{15}}{4}$），B（$\frac{9+\sqrt{15}}{4}$，$\frac{9+\sqrt{15}}{4}$）．

点评 本题考查二次函数图象的几何变换以及一次函数图象上点的坐标特征，直线和抛物线的交点问题，属于基础题．