题目内容
18．
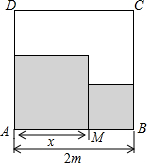如图，在边长为2m的正方形铁板内，沿着一条边恰好截取两块相邻的正方形板料，要使截取的板料面积最小，应该怎样截取？
分析 根据题意求得截取的板料面积S和x的函数解析式，根据解析式即可求得x=-$\frac{-4m}{2×2}$=m时，截取的板料面积最小．
解答 解：设截取的板料面积为S，
∴S=x2+（2m-x）2=2x2-4mx+4m2，
∵a=2＞0，
∴S有最小值，
当x=-$\frac{-4m}{2×2}$=m时，截取的板料面积最小．
点评 本题考查了二次函数的最值，二次项系数a决定二次函数图象的开口方向． ①当a＞0时，二次函数图象向上开口，函数有最小值；②a＜0时，抛物线向下开口，函数有最大值．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，△ABC中，AC边垂直平分线分别交AB、AC边于D、O两点，作CE∥AB交DO于点E，连接AE、CD．
△ABC内接于⊙O，AD平分∠BAC交⊙O于点D，DE∥AB交⊙O于E，交AC于P．求证：AC=DE；PO平分∠APD．