题目内容
20.己知抛物线y=ax2+bx+c过A(-1,0),B(3,0)C(0,3)(1)求抛物线解析式,写出对称轴及顶点D的坐标并画出函数图象.
(2)在抛物线上是否存在点P使S△PAB=6?若存在求出P点坐标,若不存在,说明理由.
分析 (1)把A(-1,0),B(3,0)C(0,3)代入y=ax2+bx+c求出a=-1,b=2,c=3,即可求出二次函数的解析式,化成顶点式即可;
(2)根据三角形的面积公式求出P点的纵坐标,代入函数的解析式求出x即可.
解答 解:(1)把A(-1,0),B(3,0)C(0,3)代入y=ax2+bx+c得:$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:a=-1,b=2,c=3,
即二次函数的解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x-1)2+4,
抛物线的对称轴是直线x=1,顶点D的坐标是(1,4),
函数的图象为: ;
;
(2)在抛物线上存在点P使S△PAB=6,
设P点的纵坐标为h,
∵A(-1,0),B(3,0),
∴AB=3-(-1)=4,
∵S△PAB=6,
∴$\frac{1}{2}$×4×|h|=6,
解得:h=±3,
把y=3代入y=-x2+2x+3得:-x2+2x+3=3,
解得:x=0或2,
把y=-3代入y=-x2+2x+3得:-x2+2x+3=-3,
解得:x=1+$\sqrt{7}$或1-$\sqrt{7}$,
所以P的坐标为(0,3)或(2,3)或(1+$\sqrt{7}$,-3)(1-$\sqrt{7}$,-3).
点评 本题考查了用待定系数法求二次函数的解析式,函数的图象,三角形的面积的应用,能求出二次函数的解析式是解此题的关键,数形结合思想的运用.

练习册系列答案
相关题目
10. 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
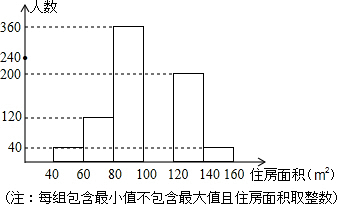
将消费者打算购买住房面积的情况整理后,作出部分频数分布直方图.
注:每组包含最小值不包含最大值,且住房面积取整数.
请你根据以上信息,回答下列问题:
(1)根据表格可得,被调查的消费者平均年收入为2.39万元;被调查的消费者中年收入的中位数是1.8;在平均数与中位数这两个数中,中位数更能反映被调查的消费者年收入的一般水平.
(2)根据频数分布直方图可得,打算购买100-120m2房子的人数为240人;打算购买住房面积小于100m2的消费者占被调查消费者人数的百分数是52%.
(3)在图中补全这个频数分布直方图.
 2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:
2013年合肥市春季房交会期间,某公司对参加本次房交会的消费者进行了随即问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 3.2 | 3.8 | 5.0 | 7.0 | 12.0 |
| 被调查的消费者数(人) | 200 | 500 | 200 | 70 | 30 |
注:每组包含最小值不包含最大值,且住房面积取整数.
请你根据以上信息,回答下列问题:
(1)根据表格可得,被调查的消费者平均年收入为2.39万元;被调查的消费者中年收入的中位数是1.8;在平均数与中位数这两个数中,中位数更能反映被调查的消费者年收入的一般水平.
(2)根据频数分布直方图可得,打算购买100-120m2房子的人数为240人;打算购买住房面积小于100m2的消费者占被调查消费者人数的百分数是52%.
(3)在图中补全这个频数分布直方图.
 已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.
如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.