题目内容
5. 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.
如图所示,在Rt△ABC中,∠C=90°,∠A=15°,BC=1,求△ABC的面积.
分析 以B为顶点作∠CBD=60°,交AC于D,根据三角形的内角和得到∠ABC=75°,于是求得∠ABD=15°,∠BDC=30°,证得AD=BD,在Rt△BDC中,CD=BC•tan60°=$\sqrt{3}$,BD=2BC=2,求得AC=2+$\sqrt{3}$,根据三角形的面积即可得到结果.
解答 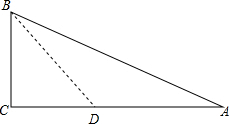 解:以B为顶点作∠CBD=60°,交AC于D,
解:以B为顶点作∠CBD=60°,交AC于D,
∵∠C=90°,∠A=15°,
∴∠ABC=75°,
∴∠ABD=15°,∠BDC=30°,
∴∠A=∠ABD,
∴AD=BD,
在Rt△BDC中,∵BC=1,
∴CD=BC•tan60°=$\sqrt{3}$,
∴BD=2BC=2,
∴AD=BD=2,
∴AC=2+$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$BC•AC=$\frac{1}{2}$×1×(2+$\sqrt{3}$)=$\frac{2+\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
15.数-3,0,$\frac{1}{2}$,-5的大小顺序是( )
| A. | -5<-3<$\frac{1}{2}$<0 | B. | 13<-5<$\frac{1}{2}$<0 | C. | -3<-5<0<$\frac{1}{2}$ | D. | -5<-3<0<$\frac{1}{2}$ |
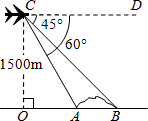 如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).
如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).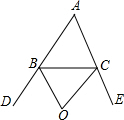 如图,BO、CO分别是△ABC的外角平分线.
如图,BO、CO分别是△ABC的外角平分线.