题目内容
11. 已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
已知,等腰△ABC中,AB=AC,点D、E分别在边BC、AC上,且∠ADE=∠C,求证:△ABD∽△DCE.
分析 根据等腰三角形的性质得∠B=∠C,由于∠ADE=∠C,所以∠ADE=∠B,再利用三角形外角性质得∠ADE+∠CDE=∠B+∠BAD,则∠BAD=∠CDE,然后根据有两组角对应相等的两个三角形相似即可得到结论.
解答 证明:∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠C,
∴∠ADE=∠B,
∵∠ADC=∠B+∠BAD,即∠ADE+∠CDE=∠B+∠BAD,
∴∠BAD=∠CDE,
∵∠B=∠C,
∴△ABD∽△DCE.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.据某市交通部门统计,该市2011年底全市汽车拥有量为150万辆,而截止到2013年底,全市的汽车拥有量已达216万辆.假定汽车拥有量年平均增长率保持不变,则2012年底该市汽车拥有量为( )
| A. | 160万辆 | B. | 170万辆 | C. | 180万辆 | D. | 200万辆 |
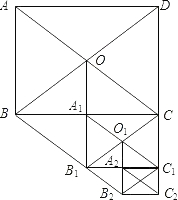 如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
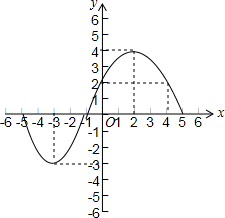 观察图,解答下列问题:
观察图,解答下列问题:
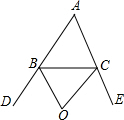 如图,BO、CO分别是△ABC的外角平分线.
如图,BO、CO分别是△ABC的外角平分线.