题目内容
 如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=
如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=考点:三角形的外角性质,三角形内角和定理
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和解答即可.
解答: 解:由三角形的外角性质得,∠1=∠B+∠F+∠C+∠G,
解:由三角形的外角性质得,∠1=∠B+∠F+∠C+∠G,
∠2=∠A+∠D,
由三角形的内角和定理得,∠1+∠2+∠F=180°,
所以,∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
故答案为:180°.
 解:由三角形的外角性质得,∠1=∠B+∠F+∠C+∠G,
解:由三角形的外角性质得,∠1=∠B+∠F+∠C+∠G,∠2=∠A+∠D,
由三角形的内角和定理得,∠1+∠2+∠F=180°,
所以,∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
故答案为:180°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
幼儿园的小朋友们打算选择一种形状、大小都相同的多边形塑胶板铺活动室的地面,为了保证铺地时既无缝隙又不重叠,请你告诉他们下面形状的塑胶板:①正三角形; ②正四边形;③正五边形;④正六边形,可以选择的是( )
| A、②③④ | B、①②③ |
| C、①②④ | D、①③④ |
在一次捐款活动中,某校七年级(1)班6名团员的捐款金额(单位:元)如下:10,15,30,50,30,20.这级数据的众数是( )
| A、10 | B、15 | C、20 | D、30 |
 已知,△ABC内接于⊙O,BC是⊙O的直径,点E在⊙O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是
已知,△ABC内接于⊙O,BC是⊙O的直径,点E在⊙O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是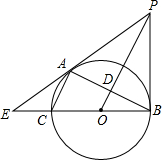 如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E.
如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 如图,折线ABC是一个路灯的示意图,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,在地面上距离A点8米的点E处,测得点B的仰角是45°,点C的仰角是60°,点E、D、A在一条直线上.求点C到地面的距离CD.(
如图,折线ABC是一个路灯的示意图,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,在地面上距离A点8米的点E处,测得点B的仰角是45°,点C的仰角是60°,点E、D、A在一条直线上.求点C到地面的距离CD.( 如图,计算所给三视图表示的几何体的体积是
如图,计算所给三视图表示的几何体的体积是 数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.
数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.