题目内容
在Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心将其按顺时针方向旋转60°到∠A′B′C′位置,则B点经过的路线长为 .
考点:弧长的计算,旋转的性质
专题:
分析:B点经过的路线长是以AB为半径,圆心角为60°的弧的长度.
解答: 解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,
解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,
∴由勾股定理知,AB=
=
=5,
则依题意得,B点经过的路线长为:
=
π.
故答案为
π.
 解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,
解:∵Rt△ABC中,∠C=90°,AC=3,BC=4,∴由勾股定理知,AB=
| AC2+BC2 |
| 32+42 |
则依题意得,B点经过的路线长为:
| 60π×5 |
| 180 |
| 5 |
| 3 |
故答案为
| 5 |
| 3 |
点评:本题考查了弧长公式:l=
(弧长为l,圆心角度数为n,圆的半径为R),勾股定理,旋转的性质,准确理解题意从而画出图形是解题的关键.
| nπR |
| 180 |

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
乔丹体育用品商店开展“超级星期六”促销活动:运动服8折出售,运动鞋每双减20元.活动期间,标价为480元的某款运动服装(含一套运动服和一双运动鞋)价格为400元.问该款运动服和运动鞋的标价各是多少元?
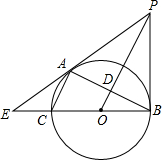 如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E.
如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 如图,计算所给三视图表示的几何体的体积是
如图,计算所给三视图表示的几何体的体积是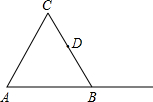 如图,△ABC是等边三角形,D是BC的中点.
如图,△ABC是等边三角形,D是BC的中点.