题目内容
在Rt△ABC中，∠C=90°，BC=5，sinA=0.7，求cosA，tanA的值．
考点：解直角三角形
专题：计算题
分析：根据三角函数的定义可得出
=0.7，从而得出AB的长，再由勾股定理得出AC的长，即可求出cosA和tanA的值．
| BC |
| AB |
解答：解：∵∠C=90°，
∴sinA=
，
∵BC=5，sinA=0.7，
∴
=0.7，
∴AB=
，
∴由勾股定理得：AC=
，
∴cosA=
=
，tanA=
=
．
∴sinA=
| BC |
| AB |
∵BC=5，sinA=0.7，
∴
| BC |
| AB |
∴AB=
| 50 |
| 7 |
∴由勾股定理得：AC=
5
| ||
| 7 |
∴cosA=
| AC |
| AB |
| ||
| 10 |
| BC |
| AC |
7
| ||
| 51 |
点评：本题考查了解直角三角形的知识，以及三角函数的定义，要熟记sinA=
，cosA=
，tanA=
．
| a |
| c |
| b |
| c |
| a |
| b |
练习册系列答案
相关题目
如图，已知△OAB∽△OCD，且DC∥AB，请写出这对相似三角形对应角和对应边的比例式．
如图，以点O为圆心的两个同心圆中，大圆的弦AB、CD是小圆的两条切线，切点分别为M、N，那么AB、CD是否相等？为什么？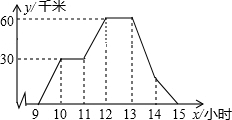
A、B两地相距60千米，图中折线表示某骑车人离A地的距离与时间的函数关系，有一辆客车9时从B地出发，以60千米/小时的速度为匀速行驶，并返往于两地之间（乘客上、下车停留时间忽略不计）