题目内容
14.计算:(1)$\frac{1}{x+1}$-$\frac{1}{x+2}$=$\frac{1}{(x+1)(x+2)}$;$\frac{1}{x+2}$-$\frac{1}{x+3}$=$\frac{1}{(x+2)(x+3)}$;$\frac{1}{x+3}$-$\frac{1}{x+4}$=$\frac{1}{(x+3)(x+4)}$;
(2)通过以上计算可以得出一定规律,请你利用以上规律化简:
$\frac{1}{a-1}$+$\frac{1}{(a-1)(a-2)}$+$\frac{1}{(a-2)(a-3)}$+…+$\frac{1}{(a-2012)(a-2013)}$.
分析 (1)根据分式的运算法则即可求出答案.
(2)根据(1)中的规律即可化简求出答案.
解答 解:(1)原式=$\frac{1}{(x+1)(x+2)}$,
原式=$\frac{1}{(x+2)(x+3)}$
原式=$\frac{1}{(x+3)(x+4)}$
(2)原式=$\frac{1}{a-1}$+$\frac{1}{a-2}$-$\frac{1}{a-1}$+$\frac{1}{a-3}$-$\frac{1}{a-2}$+…+$\frac{1}{a-2013}$-$\frac{1}{a-2012}$
=$\frac{1}{a-2013}$
故答案为:(1)$\frac{1}{(x+1)(x+2)}$;$\frac{1}{(x+2)(x+3)}$;$\frac{1}{(x+3)(x+4)}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于中等题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
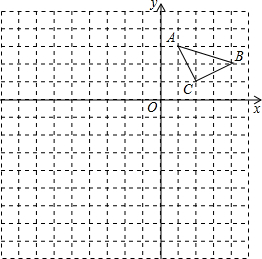 如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
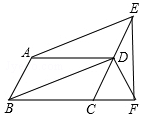 如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.