题目内容
2.如图(1),在平面直角坐标系xOy中,?OABC的顶点A的坐标为(2,0),点C的坐标为(2,2),点P在射线OA上沿OA方向以2个单位长度/s的速度向右运动,点Q在线段AB上沿AB方向以$\sqrt{2}$个单位长度/s的速度从点A向点B运动,设点Q运动的时间为t s(0≤t≤2),射线PQ交射线CB于点D,连接CP.(1)求出过O、A、B三点的抛物线的函数关系式;
(2)当0<t<1时,求出△PAQ的面积 S与t的函数关系式,并求出当t取何值时,S有最大值;
(3)在点P运动的过程中,∠CPD是一个定值,这个定值是45°;并求出当△PCD为等腰三角形时t的值;
(4)当1≤t≤2时,线段DP的中点M运动的总路程为1.
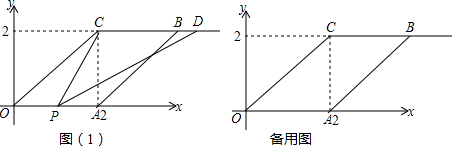
分析 (1)由题意A(2,0),C(2,2),B(4,2),设过O、A、B三点的抛物线的解析式为:y=ax(x-2),代入点B即可求出a.
(2)s=$\frac{1}{2}$•PA•QM,用t表示PA、QM代入即可.
(3)猜想是特殊角45°,由∠CPD+∠DPM=∠COP+∠OCP可知,只要证明∠OCP=∠DPM,即△PCN∽△QPM即可.
(4)观察可知点M运动路径是线段,轨迹三角形中位线定理即可解决.
解答 解:(1)如图1中,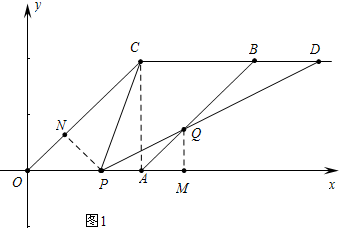 由题意A(2,0),C(2,2),B(4,2),
由题意A(2,0),C(2,2),B(4,2),
设过O、A、B三点的抛物线的解析式为:y=ax(x-2),点B代入得到a=$\frac{1}{4}$,
∴过O、A、B三点的抛物线的函数关系式为:y=$\frac{1}{4}$x2-$\frac{1}{2}$x.
(2)如图1,作QM⊥x轴垂足为M,
∵AO=OC,∠OAC=90°,
∴∠COA=45°,
∵OC∥AB,
∴∠BAM=∠COA=45°,
∵AQ=$\sqrt{2}$t,
∴AM=QM=t,
∴0<t<1时,求出△PAQ的面积 S=$\frac{1}{2}$•PA•QM=$\frac{1}{2}$•(2-2t)•t=-t2+t.
(3)如图1中,作PN⊥OC垂足为N,
∵∠PON=45°,OP=2t,
∴ON=PN=$\sqrt{2}$t,NC=2-$\sqrt{2}$t,
∵$\frac{NC}{PM}$=$\frac{2\sqrt{2}-\sqrt{2}t}{2-2t+t}$=$\sqrt{2}$,$\frac{PN}{QM}=\frac{\sqrt{2}t}{t}$=$\sqrt{2}$,
∴$\frac{NC}{PM}=\frac{PN}{QM}$,∵∠PNC=∠PMQ=90°,
∴△PCN∽△QPM,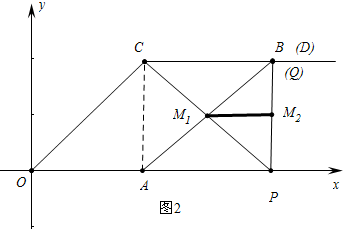
∴∠NCP=∠QPM,
∵∠CPM=∠COP+∠NCP=∠CPD+∠QPM,
∴∠CPD=45°.
故答案为45°.
①当OP=OA时△PCD是等腰三角形,此时:2t=2,t=1.
②当OP=OC时△PCD是等腰三角形,此时2t=2$\sqrt{2}$,t=$\sqrt{2}$.
③当OP=2OA时△PCD是等腰三角形,此时2t=4,t=2.
综上所述:t=1s或$\sqrt{2}$s或2s时,△PCD是等腰三角形.
(4)如图2中,点M运动的轨迹是线段M1M2,
∵AM1=BM1,PM2=BM2,
∴M1M2=$\frac{1}{2}$AP=1.
故答案为1.
点评 本题考查待定系数法求二次函数解析式、相似三角形的判定和性质、等腰三角形的判定和性质等知识,学会猜想,分类讨论的思想是解决问题的关键.

| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 3,4,6 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ | D. | $\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$ |

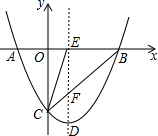 如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).
如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).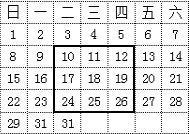 如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).
如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).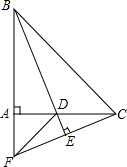 已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.