题目内容
20.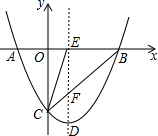 如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).
如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).(1)求出该二次函数解析式及其顶点D的坐标;
(2)求出点B的坐标;
(3)当y随x增大而减小时,x的取值范围是x<1;
(4)直接写出△CEF的面积是1.
分析 (1)根据待定系数法以及配方法即可解决.
(2)令y=0解方程即可.
(3)根据二次函数增减性回答即可.
(4)先求出直线BC,再求出的F坐标即可求出△CEF的面积.
解答 解:(1)由二次函数y=x2+bx+c经过A(-1,0),C(0,-3),得$\left\{\begin{array}{l}{c=-3}\\{1-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
所以抛物线为:y=x2-2x-3,
∵y=x2-2X-3=(x-1)2-4,
∴顶点D(1,-4).
(2)令y=0则x2-2x-3=0,解得x=3或-1,所以点B(3,0).
(3)x<1时,当y随x增大而减小,
故答案为x<1.
(4)设直线BC为y=kx+b,
∵直线BC经过B(3,0),C(0,-3),
∴$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$.
∴直线BC为y=x-3,
∴F(1,-2),E(1,0),
∴S△EFC=$\frac{1}{2}$×2×1=1.
故答案为1.
点评 本题考查待定系数法求二次函数解析式,用配方法求顶点坐标,利用图象确定函数值的增减性等知识,灵活运用这些知识是解决问题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,DE∥BC交AB、AC于点D、E,AE=3,AC=5,DE=4,那么BC=$\frac{20}{3}$.
如图,在△ABC中,DE∥BC交AB、AC于点D、E,AE=3,AC=5,DE=4,那么BC=$\frac{20}{3}$.
 如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.
如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.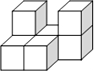 如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )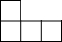



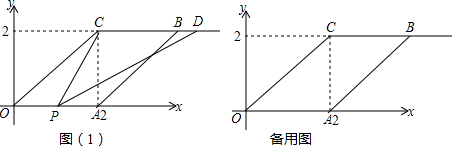
 如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论: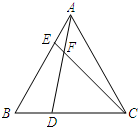 如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.
如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.