Question

2．如图，直线L：y=-x+3与x轴、y轴分别交于A、B两点，在x轴上有一动点M从原点O出发以每秒1个单位的速度向左移动．
（1）求A、B两点的坐标；
（2）求△ABM的面积S与M的移动时间t的函数关系式；
（3）在M移动的过程中是否存在某个时刻能使△ABM是等腰三角形？若能，求出t的值，并求此时M点的坐标；若不能，请说明理由．

Answer 1

分析 （1）由直线l解析式，分别令x与y为0求出对应y与x的值，确定出A与B坐标即可；
（2）如图1所示，由M点运动的时间与速度表示出OM的长，由OM+OA求出AM的长，再由BO垂直于AM，表示出S与t的函数关系式即可；
（3）在M移动的过程中存在某个时刻能使△ABM是等腰三角形，如图2所示，分三种情况考虑：当BM₁=BA时，由对称性可得M₁坐标；当AB=AM₂时，由AM₂-OA求出OM₂的长，表示出M₂坐标；当AM₃=BM₃时，M₃与原点O重合，求出此时M₃的坐标即可．

解答 解：（1）对于直线l：y=-x+3，
令x=0，得到y=3；令y=0，得到x=3，
则A（3，0），B（0，3）；
（2）如图1所示：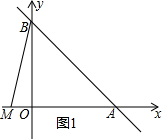

由题意得：OM=t，OA=OB=3，
∴AM=OA+OM=t+3，
则△ABM的面积S与M的移动时间t的函数关系式为S=$\frac{1}{2}$（t+3）×3=$\frac{3}{2}$t+$\frac{9}{2}$；
（3）在M移动的过程中存在某个时刻能使△ABM是等腰三角形，如图2所示，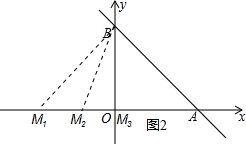

分三种情况考虑：当BM₁=BA时，由对称性可得M₁（-3，0）；
当AB=AM₂=3$\sqrt{2}$时，OM₂=AM₂-OA=3$\sqrt{2}$-3，此时M₂（3-3$\sqrt{2}$，0）；
当AM₃=BM₃时，M₃与原点O重合，此时M₃（0，0）．

点评 此题属于一次函数综合题，涉及的知识有：一次函数与坐标轴的交点，坐标与图形性质，等腰三角形的性质，勾股定理，熟练掌握一次函数的性质是解本题的关键．