题目内容
12.已知在数轴上点A表示-3,点B表示2,点D是AB的中点,点C是数轴上的点,且满足CB=2AC,则CD两点之间的距离是7.5或$\frac{5}{6}$.分析 根据CB=2AC,可得C点坐标,根据线段的和差,可得答案.
解答 解:当C在线段AB上时,由线段的和差,得
AC+CB=AB,即AC+2AC=BC=2-(-3)=5,
解得AC=$\frac{5}{3}$.
由线段的和差,得CD=AD-AC=$\frac{5}{2}$-$\frac{5}{3}$=$\frac{5}{6}$;
当C在线段AB的延长线上时,由线段的和差,得
AC+AB=CB,即AC+[2-(-3)]=2AC.
解得AC=5,
CD=AC+AD=5+$\frac{5}{2}$=7.5,
CD两点之间的距离是7.5或 $\frac{5}{6}$,
故答案为:7.5或 $\frac{5}{6}$.
点评 本题考查了两点间的距离,利用线段的和差得出关于AC的方程是解题关键,要分类讨论,以防遗漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知点A,B,C在同一直线上,AB=4cm,AC=3cm,则B、C两点之间的距离是( )
| A. | 1cm | B. | 5cm | C. | 7cm | D. | 1cm或7cm |
17.点B(0,-3)在( )
| A. | x轴的正半轴上 | B. | x轴的负半轴上 | C. | y轴的正半轴上 | D. | y轴的负半轴上 |
2.函数y=$\frac{\sqrt{x-3}}{x-2}$的自变量x的取值范围是( )
| A. | x≠2 | B. | x≥3 | C. | x>3且x≠2 | D. | x≥3且x≠2 |
 已知:抛物线C1:y=(x+1)2+1
已知:抛物线C1:y=(x+1)2+1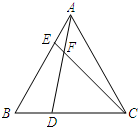 如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.
如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE. 如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
如图,已知一次函数y=-$\frac{1}{2}$x+2的图象分别交x轴,y轴于B点、A点,抛物线y=ax2+$\frac{1}{2}$x+c的图象经过A、B两点,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.