题目内容
3.解方程组:$\left\{\begin{array}{l}x+y=5\\{x^2}-3xy+2{y^2}=0\end{array}\right.$.分析 将方程②因式分解后可得x=y或x=2y,分别代入方程①可得方程组的两组解.
解答 解:$\left\{\begin{array}{l}{x+y=5}&{①}\\{{x}^{2}-3xy+2{y}^{2}=0}&{②}\end{array}\right.$,
由②可得:(x-y)(x-2y)=0,即x-y=0或x-2y=0,
可得x=y或x=2y,
将x=y代入①,得:2y=5,y=$\frac{5}{2}$,
故$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{5}{2}}\end{array}\right.$;
将x=2y代入①,得:3y=5,y=$\frac{5}{3}$,
则x=$\frac{10}{3}$,
故$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{5}{3}}\end{array}\right.$;
综上,$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{5}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{5}{3}}\end{array}\right.$.
点评 本题主要考查解高次方程的能力,解高次方程的根本思想是化归思想,次数较高可通过分解等方法降幂求解即可.

练习册系列答案
相关题目
14.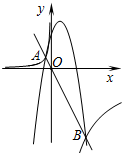 如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )
如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )
 如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )
如图,直线y=-2x与抛物线y=-x2+mx+6交于A、B两点,过A、B两点的双曲线的解析式分别为$y=\frac{k_1}{x}$、$y=\frac{k_2}{x}$,则k1k2的值为( )| A. | -6 | B. | 36 | C. | 72 | D. | 144 |
11.下列计算结果正确的是( )
| A. | a4•a2=a8 | B. | (a4)2=a6 | C. | (ab)2=a2b2 | D. | (a-b)2=a2-b2 |
8.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. | 正五边形 | B. | 正六边形 | C. | 等腰三角形 | D. | 等腰梯形 |