题目内容
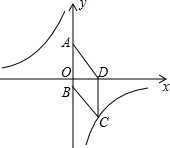 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COB的面积相等.求点P的坐标.
考点:菱形的性质,待定系数法求反比例函数解析式
专题:
分析:(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;
(2)设出点P的坐标,易得△COB的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,继而可求得点P的坐标.
(2)设出点P的坐标,易得△COB的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,继而可求得点P的坐标.
解答:解:(1)由题意知,OA=4,OD=3
在Rt△AOB中,AD=
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=CD=5,
∴C(3,-5).
设经过点C的反比例函数的解析式为y=
(k≠0),
则
=-5,
解得:k=-15.
故所求的反比例函数的解析式为y=-
;
(2)设P(x,y)
∵AD=AB=5,OA=4,
∴OB=1,S△COB=
×1×3=
,
即
×OA×|x|=
,
∴|x|=
,
∴x=±
,
此时y=±
,
故点P的坐标为(
,-
),(-
,
).
在Rt△AOB中,AD=
| 32+42 |
∵四边形ABCD为菱形,
∴AD=BC=AB=CD=5,
∴C(3,-5).
设经过点C的反比例函数的解析式为y=
| k |
| x |
则
| k |
| 3 |
解得:k=-15.
故所求的反比例函数的解析式为y=-
| 15 |
| x |
(2)设P(x,y)
∵AD=AB=5,OA=4,
∴OB=1,S△COB=
| 1 |
| 2 |
| 3 |
| 2 |
即
| 1 |
| 2 |
| 3 |
| 2 |
∴|x|=
| 3 |
| 4 |
∴x=±
| 4 |
| 3 |
此时y=±
| 45 |
| 4 |
故点P的坐标为(
| 3 |
| 2 |
| 45 |
| 4 |
| 3 |
| 2 |
| 45 |
| 4 |
点评:本题考查了菱形的性质以及待定系数法求反比例函数解析式,根据菱形的四条边相等的性质得到点C的坐标,注意:点P的横坐标的有两种情况.

练习册系列答案
相关题目
已知抛物线y=x2-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A、2013 | B、2015 |
| C、2014 | D、2010 |
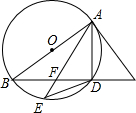 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.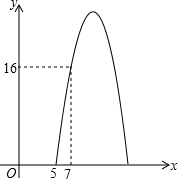 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.

