题目内容
在矩形ABCD中,AB=4,BC=5,P是射线BC上的一个动点,作PE⊥AP,PE交射线DC于点E,射线AE交射线BC于点F,设BP=x,CF=y.
(1)当sin∠APB=
时,求CE的长;
(2)如图,当点P在边BC上时(点P与点B、C不重合),求y关于x的函数关系式,并写出它的定义域;
(3)当
=
时,求CF的长.

(1)当sin∠APB=
| 4 |
| 5 |
(2)如图,当点P在边BC上时(点P与点B、C不重合),求y关于x的函数关系式,并写出它的定义域;
(3)当
| PE |
| AP |
| 1 |
| 2 |

考点:相似三角形的判定与性质,勾股定理,矩形的性质
专题:
分析:(1)根据矩形的性质和垂直的性质即可证明△PCE∽△ABP,根据相似三角形对应边成比例即可求得CE的长;
(2)根据EC∥AB,求得△ECF∽△ABF,得出FC:FB=EC:AB,再利用(1)中相似三角形的性质即可证明CE:BP=PC:AB,从而求得y关于x的函数关系式.
(3)根据△PCE∽△ABP,得出
=
=
=
,从而求得PC=2,PB=3,进而求得CE=
,然后根据AB∥CD,得出
=
,从而求得CF的长.
(2)根据EC∥AB,求得△ECF∽△ABF,得出FC:FB=EC:AB,再利用(1)中相似三角形的性质即可证明CE:BP=PC:AB,从而求得y关于x的函数关系式.
(3)根据△PCE∽△ABP,得出
| PC |
| AB |
| CE |
| BP |
| PE |
| AP |
| 1 |
| 2 |
| 3 |
| 2 |
| CF |
| BF |
| CE |
| AB |
解答:解:(1)在RT△APB中,AB=4,sin∠APB=
,
∴sin∠APB=
=
,
∴AP=5,
∴PB=
=3,
∴PC=BC-PB=5-3=2,
在矩形ABCD中,
∵PE⊥AP,
∴∠CPE+∠APN=90°,
∵∠BAP+∠APB=90°,
∴∠CPE=∠BAP,
∵∠ECP=∠B=90°,
∴△PCE∽△ABP;
∴CE:BP=PC:AB,
∴CE=
=
=
.
(2)∵EC∥AB,
∴△ECF∽△ABF,
∴FC:FB=EC:AB,
∵△PCE∽△ABP,
∴CE:BP=PC:AB,
即CE=
,
∴
=
,
整理得,y=-
,
∴y关于x的函数关系式为y=-
(0<x<5).
(3)∵△PCE∽△ABP,
∴
=
=
=
,
∴PC=2,PB=3,
∴CE=
,
∵AB∥CD,
∴
=
,
即
=
,
解得CF=3.
| 4 |
| 5 |
∴sin∠APB=
| AB |
| AP |
| 4 |
| 5 |
∴AP=5,
∴PB=
| AP2-AB2 |
∴PC=BC-PB=5-3=2,
在矩形ABCD中,
∵PE⊥AP,
∴∠CPE+∠APN=90°,
∵∠BAP+∠APB=90°,
∴∠CPE=∠BAP,
∵∠ECP=∠B=90°,
∴△PCE∽△ABP;
∴CE:BP=PC:AB,
∴CE=
| PC•BP |
| AB |
| 2×3 |
| 5 |
| 6 |
| 5 |
(2)∵EC∥AB,
∴△ECF∽△ABF,
∴FC:FB=EC:AB,
∵△PCE∽△ABP,
∴CE:BP=PC:AB,
即CE=
| x(5-x) |
| 5 |
∴
| y |
| 5+y |
| x(5-x) |
| 52 |
整理得,y=-
| 5(x2-5x) |
| x2-5x+16 |
∴y关于x的函数关系式为y=-
| 5(x2-5x) |
| x2-5x+16 |
(3)∵△PCE∽△ABP,
∴
| PC |
| AB |
| CE |
| BP |
| PE |
| AP |
| 1 |
| 2 |
∴PC=2,PB=3,
∴CE=
| 3 |
| 2 |
∵AB∥CD,
∴
| CF |
| BF |
| CE |
| AB |
即
| CF |
| 5+CF |
| ||
| 4 |
解得CF=3.
点评:本题考查相似三角形的判定和性质,勾股定理以及矩形的性质.三角形相似的判定和性质是本题的重点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
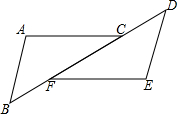 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.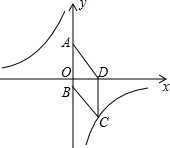 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).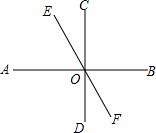 如图,已知直线AB,CD,EF相交于点O,CD⊥AB,∠DOF:∠AOD=1:3,求∠COE和∠AOE的度数.
如图,已知直线AB,CD,EF相交于点O,CD⊥AB,∠DOF:∠AOD=1:3,求∠COE和∠AOE的度数. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,△OEB的面积为
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,△OEB的面积为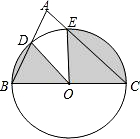 如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)
如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)