题目内容
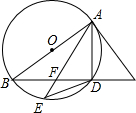 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
考点:切线的性质
专题:计算题
分析:(1)由切线的性质得BA⊥AC,则∠2+∠BAD=90°,再根据圆周角定理得∠ADB=90°,则∠B+∠BAD=90°,所以∠B=∠2,接着由DA=DE得到∠1=∠E,由圆周角定理得∠B=∠E,所以∠1=∠2,可判断AF=AC,根据等腰三角形的性质得FD=DC;
(2)作DH⊥AE于H,如图,根据等腰三角形的性质得AH=EH=
AE=4,再根据勾股定理可计算出DH=3,然后证明△BDA∽△EHD,利用相似比可计算出AB=
,从而可得⊙O的半径.
(2)作DH⊥AE于H,如图,根据等腰三角形的性质得AH=EH=
| 1 |
| 2 |
| 25 |
| 3 |
解答:(1)证明:∵AC是⊙O的切线,
∴BA⊥AC,
∴∠2+∠BAD=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B=∠2,
∵DA=DE,
∴∠1=∠E,
而∠B=∠E,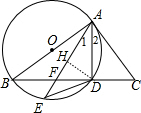
∴∠B=∠1,
∴∠1=∠2,
∴AF=AC,
而AD⊥CF,
∴FD=DC;
(2)解:作DH⊥AE于H,如图,
∵DA=DE=5,
∴AH=EH=
AE=4,
在Rt△DEH中,DH=
=3,
∵∠B=∠E,∠ADB=∠DHE=90°,
∴△BDA∽△EHD,
∴
=
,即
=
,
∴AB=
,
∴⊙O的半径为
.
∴BA⊥AC,
∴∠2+∠BAD=90°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠B=∠2,
∵DA=DE,
∴∠1=∠E,
而∠B=∠E,

∴∠B=∠1,
∴∠1=∠2,
∴AF=AC,
而AD⊥CF,
∴FD=DC;
(2)解:作DH⊥AE于H,如图,
∵DA=DE=5,
∴AH=EH=
| 1 |
| 2 |
在Rt△DEH中,DH=
| DE2-EH2 |
∵∠B=∠E,∠ADB=∠DHE=90°,
∴△BDA∽△EHD,
∴
| AB |
| DE |
| AD |
| DH |
| AB |
| 5 |
| 5 |
| 3 |
∴AB=
| 25 |
| 3 |
∴⊙O的半径为
| 25 |
| 6 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的判定与性质、圆周角定理、勾股定理和相似三角形的判定与性质.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.
如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.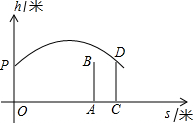 甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是
甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是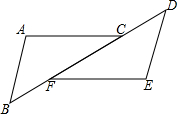 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.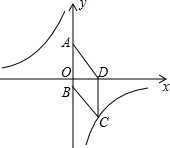 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).