题目内容
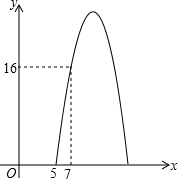 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.(1)求y与x之间的函数关系式.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)销售单价在什么范围时,该种商品每天的销售利润不低于16元?(直接写出答案)
考点:二次函数的应用
专题:
分析:(1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)利用二次函数对称性得出每天的销售利润不低于16元时x的取值范围即可.
(2)利用配方法求出二次函数最值即可;
(3)利用二次函数对称性得出每天的销售利润不低于16元时x的取值范围即可.
解答:解:(1)y=ax2+bx-75图象过点(5,0)、(7,16),
∴
,
解得:
.
故y=-x2+20x-75;
(2)y=-x2+20x-75=-(x-10)2+25,则其顶点坐标是(10,25),
当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;
(3)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.
∴
|
解得:
|
故y=-x2+20x-75;
(2)y=-x2+20x-75=-(x-10)2+25,则其顶点坐标是(10,25),
当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;
(3)∵函数y=-x2+20x-75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=-x2+20x-75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.
点评:此题主要考查了二次函数的应用以及待定系数法求二次函数解析式等知识,正确利用二次函数对称性得出是解题关键.

练习册系列答案
相关题目
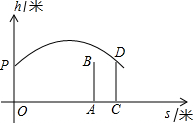 甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是
甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞出的水平距离s(米)与其距地面高度h(米)之间的关系式为h=-s2+5s+8.如图,球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是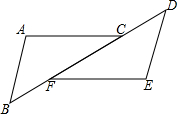 如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.
如图∠A=∠E,AB∥DE,BF=CD,说明AC与EF的关系.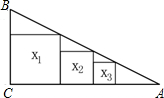 如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题:
如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3…,xn的n个正方形依次放入△ABC中,请回答下列问题: 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.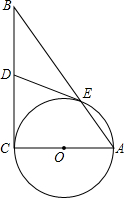 如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,
如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,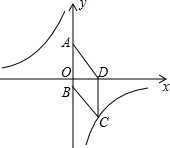 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).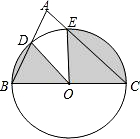 如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)
如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=72°,BC=4.求图中阴影部分的总周长和总面积(结果保留π)