题目内容
1. 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
分析 可先证明Rt△ACB≌Rt△B′CO,从而可知阴影部分的面积等于圆面积的$\frac{1}{6}$;如图2,阴影部分的面积=圆的面积-S1-S2.
解答 解:如图1,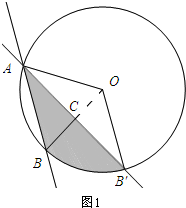 当点B运动到点B′的位置时,过点O作OC⊥AB′,
当点B运动到点B′的位置时,过点O作OC⊥AB′,
∵AB=AO=BO=1,
∴∠AOB=60°.
由垂径定理可知:AC=CB′=$\frac{\sqrt{3}}{2}$,
由锐角三角形函数的定义可知:sin∠AOC=$\frac{AC}{AO}$=$\frac{\frac{\sqrt{3}}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
∴∠AOC=60°.
∴点O、C、B在同一条直线上.
在Rt△ACB和Rt△B′CO中
∵$\left\{\begin{array}{l}AB=OB′\\ AC=CB′\end{array}\right.$,
∴Rt△ACB≌Rt△B′CO(HL).
∴直线AB扫过的面积=扇形BOB′的面积=$\frac{1}{6}$π×12=$\frac{π}{6}$. 如图2:当点B运动到点B′的位置时,过点O作OC⊥AB′,
如图2:当点B运动到点B′的位置时,过点O作OC⊥AB′,
∵AB=AO=BO=1,
∴∠AOB=60°.
∴S2=扇形AOB的面积-△AOB的面积=$\frac{1}{6}$π×12-$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{π}{6}$-$\frac{\sqrt{3}}{4}$;
S1=扇形AOB′的面积-△AOB′的面积=$\frac{1}{3}$π×12-$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$;
∴直线AB扫过的面积=圆的面积-S1-S2=π-($\frac{π}{6}$-$\frac{\sqrt{3}}{4}$)-($\frac{π}{3}$-$\frac{\sqrt{3}}{4}$)=π-$\frac{π}{6}$+$\frac{\sqrt{3}}{4}$-$\frac{π}{3}$+$\frac{\sqrt{3}}{4}$=$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
点评 本题主要考查的是旋转的性质,扇形的面积公式,将不规则图形的面积转为规则图形的面积是解题的关键.

 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )| A. | $\frac{9\sqrt{3}}{10}$cm | B. | $\frac{18\sqrt{3}}{10}$cm | C. | $\frac{9\sqrt{3}}{5}$cm | D. | $\frac{18\sqrt{3}}{5}$cm |

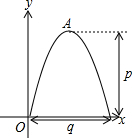 如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.
如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.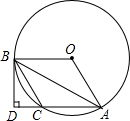 如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D.
如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D. 课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.