题目内容
楚天汽车销售公司5月份销售某种型号汽车，当月该型号汽车的进价为30万元/辆，若当月销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0.1万元/辆．根据市场调查，月销售量不会突破30台．
（1）设当月该型号汽车的销售量为x辆（x≤30，且x为正整数），实际进价为y万元/辆，求y与x的函数关系式；
（2）已知该型号汽车的销售价为32万元/辆，公司计划当月销售利润25万元，那么该月需售出多少辆汽车？（注：销售利润=销售价-进价）
（1）设当月该型号汽车的销售量为x辆（x≤30，且x为正整数），实际进价为y万元/辆，求y与x的函数关系式；
（2）已知该型号汽车的销售价为32万元/辆，公司计划当月销售利润25万元，那么该月需售出多少辆汽车？（注：销售利润=销售价-进价）
考点：一元二次方程的应用,分段函数
专题：销售问题
分析：（1）根据分段函数可以表示出当0＜x≤5，5＜x≤30时由销售数量与进价的关系就可以得出结论；
（2）由销售利润=销售价-进价，由（1）的解析式建立方程就可以求出结论．
（2）由销售利润=销售价-进价，由（1）的解析式建立方程就可以求出结论．
解答：解：（1）由题意，得
当0＜x≤5时
y=30．
当5＜x≤30时，
y=30-0.1（x-5）=-0.1x+30.5．
∴y=
；
（2）当0＜x≤5时，
（32-30）×5=10＜25，不符合题意，
当5＜x≤30时，
[32-（-0.1x+30.5）]x=25，
解得：x1=-25（舍去），x2=10．
答：该月需售出10辆汽车．
当0＜x≤5时
y=30．
当5＜x≤30时，
y=30-0.1（x-5）=-0.1x+30.5．
∴y=
|
（2）当0＜x≤5时，
（32-30）×5=10＜25，不符合题意，
当5＜x≤30时，
[32-（-0.1x+30.5）]x=25，
解得：x1=-25（舍去），x2=10．
答：该月需售出10辆汽车．
点评：本题考查了分段函数的运用，一元二次方程的解法的运用，解答时求出分段函数的解析式是关键．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
如图，直线a∥b，直线c与直线a，b都相交，∠1=65°，则∠2=
关于x的反比例函数y=四边形ABCD中，对角线AC=BD，点E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是（ ）
| A、正方形 | B、矩形 |
| C、等腰梯形 | D、菱形 |
抛物线y=（x-1）2+2与y轴交点坐标为（ ）
| A、（0，1） |
| B、（0，2） |
| C、（1，2） |
| D、（0，3） |
钓鱼岛自古以来就是中国的领土．如图，我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航，某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处，这时两船同时接到立即赶往C处海域巡查的任务，并测得C处位于A处北偏东59°方向、位于B处北偏西44°方向．若甲、乙两船分别沿AC，BC方向航行，其平均速度分别是20海里/小时，18海里/小时，试估算哪艘船先赶到C处．
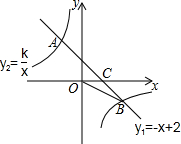如图，一次函数y1=-x+2的图象与反比例函数y2=