题目内容
 关于x的反比例函数y=
关于x的反比例函数y=| a+4 |
| x |
| 1 |
| 4 |
考点:根的判别式,反比例函数的性质
专题:压轴题,判别式法
分析:由比例函数y=
的图象位于一、三象限得出a+4>0,A、P为该图象上的点,且关于原点成中心对称,得出2xy>12,进一步得出a+4>6,由此确定a的取值范围,进一步利用根的判别式判定方程根的情况即可.
| a+4 |
| x |
解答:解:∵反比例函数y=
的图象位于一、三象限,
∴a+4>0,
∴a>-4,
∵A、P关于原点成中心对称,PB∥y轴,AB∥x轴,△PAB的面积大于12,
∴2xy>12,
即a+4>6,a>2
∴a>2.
∴△=(-1)2-4(a-1)×
=2-a<0,
∴关于x的方程(a-1)x2-x+
=0没有实数根.
故答案为:没有实数根.
| a+4 |
| x |
∴a+4>0,
∴a>-4,
∵A、P关于原点成中心对称,PB∥y轴,AB∥x轴,△PAB的面积大于12,
∴2xy>12,
即a+4>6,a>2
∴a>2.
∴△=(-1)2-4(a-1)×
| 1 |
| 4 |
∴关于x的方程(a-1)x2-x+
| 1 |
| 4 |
故答案为:没有实数根.
点评:此题综合考查了反比例函数的图形与性质,一元二次方程根的判别式,注意正确判定a的取值范围是解决问题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
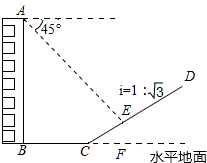 如图,一楼房AB后有一假山,其坡度为i=1:
如图,一楼房AB后有一假山,其坡度为i=1: 如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是
如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是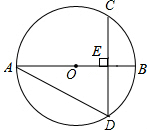 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD=
如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD=