题目内容
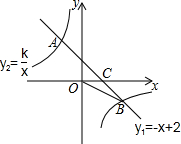 如图,一次函数y1=-x+2的图象与反比例函数y2=
如图,一次函数y1=-x+2的图象与反比例函数y2=| k |
| x |
| 1 |
| 2 |
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)作BD⊥x轴于D,如图,在Rt△OBD中,根据正切的定义得到tan∠BOC=
=
,则
=
,即m=-2n,再把点B(m,n)代入y1=-x+2得n=-m+2,然后解关于m、n的方程组得到n=-2,m=4,即B点坐标为(4,-2),再把B(4,-2)代入y2=
可计算出k=-8,所以反比例函数解析式为y2=-
;
(2)观察函数图象得到当x<4,y2的取值范围为y2>0或y2<-2.
| BD |
| OD |
| 1 |
| 2 |
| -n |
| m |
| 1 |
| 2 |
| k |
| x |
| 8 |
| x |
(2)观察函数图象得到当x<4,y2的取值范围为y2>0或y2<-2.
解答: 解:(1)作BD⊥x轴于D,如图,
解:(1)作BD⊥x轴于D,如图,
在Rt△OBD中,tan∠BOC=
=
,
∴
=
,即m=-2n,
把点B(m,n)代入y1=-x+2得n=-m+2,
∴n=2n+2,解得n=-2,
∴m=4,
∴B点坐标为(4,-2),
把B(4,-2)代入y2=
得k=4×(-2)=-8,
∴反比例函数解析式为y2=-
;
(2)当0<x<4时,y2的取值范围是y2<-2,当x<0时,y2>0.
 解:(1)作BD⊥x轴于D,如图,
解:(1)作BD⊥x轴于D,如图,在Rt△OBD中,tan∠BOC=
| BD |
| OD |
| 1 |
| 2 |
∴
| -n |
| m |
| 1 |
| 2 |
把点B(m,n)代入y1=-x+2得n=-m+2,
∴n=2n+2,解得n=-2,
∴m=4,
∴B点坐标为(4,-2),
把B(4,-2)代入y2=
| k |
| x |
∴反比例函数解析式为y2=-
| 8 |
| x |
(2)当0<x<4时,y2的取值范围是y2<-2,当x<0时,y2>0.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是
如图,在数轴上,从原点A开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;…按此规律,继续画等边三角形,那么第五个等边三角形的面积是
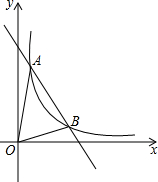 如图,一次函数y=kx+b与反比例函数
如图,一次函数y=kx+b与反比例函数 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分):
某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表(单位:分): 如图,轮船从点A处出发,先航行至位于点A的南偏西15°且与点A相距100km的点B处,再航行至位于点B的北偏东75°且与点B相距200km的点C处.
如图,轮船从点A处出发,先航行至位于点A的南偏西15°且与点A相距100km的点B处,再航行至位于点B的北偏东75°且与点B相距200km的点C处.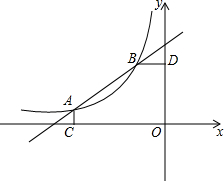 如图,已知A(-4,
如图,已知A(-4,