题目内容
17. 如图,港口A在观测站O的正东方向,某船从港口A出发,沿北偏东15°方向航行2km到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则观测站O距港口A的距离(即OA的长)为( )
如图,港口A在观测站O的正东方向,某船从港口A出发,沿北偏东15°方向航行2km到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则观测站O距港口A的距离(即OA的长)为( )| A. | $\sqrt{2}$km | B. | 2km | C. | 2$\sqrt{2}$km | D. | 4$\sqrt{2}$km |
分析 过点A作AD⊥OB于D.先求出∠B的度数,再求出AD的长,在Rt△OAD中,可求出OA的长.
解答 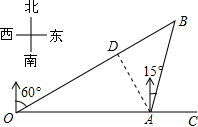 解:如图,过点A作AD⊥OB于D.
解:如图,过点A作AD⊥OB于D.
在Rt△AOD中,
∠B=180°-30°-90°-15°=45°,
∴AD=AB•sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$km,
∴OA=2×$\sqrt{2}$=2$\sqrt{2}$km.
即该船航行的距离(即OA的长)为2$\sqrt{2}$km.
故选C.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在“百度”搜索引擎中输入“雾霾天气形成的原因”,搜索的相关结果约为6430000,将数字6430000用科学记数法表示为( )
| A. | 6.43×105 | B. | 0.643×107 | C. | 64.3×105 | D. | 6.43×106 |
7.下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
| A. | a=3,b=4,c=5 | B. | a=5,b=12,c=13 | ||
| C. | a=1,b=3,c=$\sqrt{10}$ | D. | a=$1\frac{3}{7}$,b=$1\frac{4}{7}$,c=$1\frac{5}{7}$ |

 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.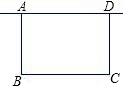 如图,学校准备利用图书馆后面的场地用围栏圈建一个面积为60平方米的长方形ABCD,车棚的一边利用图书馆的后墙,墙长为a.
如图,学校准备利用图书馆后面的场地用围栏圈建一个面积为60平方米的长方形ABCD,车棚的一边利用图书馆的后墙,墙长为a.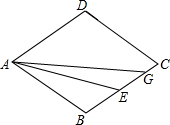 如图,在菱形ABCD中,点E为BC的中点,点G在BC边上,连结AE,AG.
如图,在菱形ABCD中,点E为BC的中点,点G在BC边上,连结AE,AG. 如图,AB⊥DB,CD⊥DB,∠1=∠2.射线BE与DF是否平行?请说明理由.
如图,AB⊥DB,CD⊥DB,∠1=∠2.射线BE与DF是否平行?请说明理由.