Question

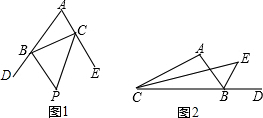
6．如图，AB⊥DB，CD⊥DB，∠1=∠2．射线BE与DF是否平行？请说明理由．

Answer 1

分析 根据垂直定义可得∠ABD=∠BDC=90°，再根据等角的余角相等可得∠EBD=∠FDB，再根据内错角相等两直线平行可得BE∥DF．

解答 解：BE∥DF，
∵AB⊥DB，CD⊥DB，
∴∠ABD=∠BDC=90°，
∵∠1=∠2，
∴∠EBD=∠FDB，
∴BE∥DF．

点评 此题主要考查了平行线的判定，关键是掌握内错角相等两直线平行．