题目内容
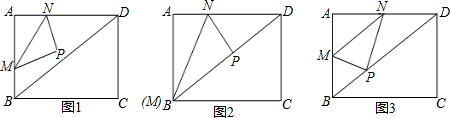
4.如图1,在矩形纸片ABCD中,已知AB=3,BC=4,M、N分别是边AB、AD上的动点.现将纸片沿MN折叠,得到△MNP.(1)若点P在对角线BD上.
①如图2,若M点与B点重合时,求AN的长;
②如图3,若MN∥BD,判断以MN为直径的圆与直线BD的位置关系,并说明理由.
(2)若BM=AN,以MN为直径的圆能否与直线BD相切?若能,请求出AN的长;若不能,请说明理由.
分析 (1)根据翻折的性质,可得AN与PN的关系,根据三角形的面积公式,可得关于AN的方程;
(2)根据直角三角形的性质,可得OP与MN的关系,根据直角三角形三边的关系,可得答案;
(3)根据相似三角形的判定与性质,可得答案.
解答 解:(1)由翻折的性质,得
AN=PN.
由勾股定理,得
BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5,
由S△ABD=$\frac{1}{2}$AB•AD=S△ABN+S△BND,得
$\frac{1}{2}$×3AN+$\frac{1}{2}$×5NP=$\frac{1}{2}$×3×4,即$\frac{3}{2}$AN+$\frac{5}{2}$AN=6.
解得AN=$\frac{3}{2}$;
(2)如图1:O为圆心,作OE⊥BD于E,连接OP, ,
,
由直角三角形的性质,得
OP=OM=ON,
由直角三角形三边的关系,得
OP>OE,
⊙O与直线BD相交;
(3)当M与A重合时,如图2 ,
,
$\frac{OP}{AB}$=$\frac{OD}{BD}$,AN=BM=3,OP=$\frac{3}{2}$
即⊙O与直线BD相切.
点评 本题考查了圆的综合题,利用了翻折的性质,直线与圆的位置关系,圆心到直线的距离等于半径;直线与圆相切,圆心到直线的距离小于半径,直线与圆相交.

练习册系列答案
相关题目
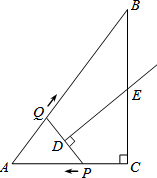 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).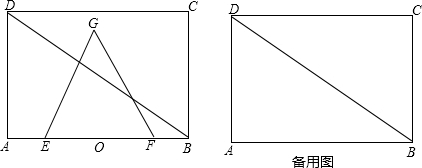
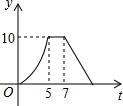
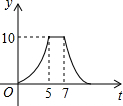
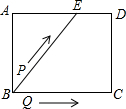 如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )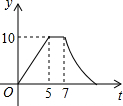

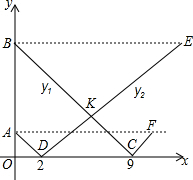 甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.
甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.