题目内容
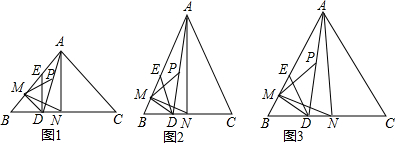
3.△ABC中,AB=AC,点D在BC上,E在AB上,BD=DE,连接AD,点P,M,N分别是AD,BE,BC的中点,连接DM,AN.(1)如图1,若∠BAC=90°,则∠PMN=45°;
(2)如图2,若∠BAC=60°,则∠PMN=60°;
(3)如图3,若∠BAC=α,则∠PMN=90°-$\frac{1}{2}α$,请证明.
分析 连接PN,首先根据等腰三角形的性质可得DM⊥BE,进而可得△AMD是直角三角形,再根据直角三角形的性质可得PM=PA=$\frac{1}{2}$AD,再根据AB=AC,N是BC中点可得△ADN是直角三角形,进而可得PN=PA=$\frac{1}{2}$AD,可证明点P是△AMN的外心,则∠PMN=∠PNM=$\frac{1}{2}$(180°-2∠MAN)=90°-∠MAN=90°-$\frac{1}{2}$∠BAC,然后再把(1)(2)(3)中∠BAC的度数分别代入即可.
解答 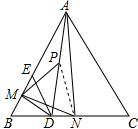 解:连接PN,
解:连接PN,
∵BD=DE,M是BE的中点,
∴DM⊥BE,
∴△AMD是直角三角形,
∵P是AD的中点,
∴PM=PA=$\frac{1}{2}$AD,
∵AB=AC,N是BC中点,
∴AN⊥BC,
∴△ADN是直角三角形,
∴PN=PA=$\frac{1}{2}$AD,
∴PA=PM=PN,
∴点P是△AMN的外心,
∴∠PMN=∠PNM=$\frac{1}{2}$(180°-2∠MAN)=90°-∠MAN=90°-$\frac{1}{2}$∠BAC,
(1)∵∠BAC=90°,
∴∠PMN=90°-$\frac{1}{2}×90°$=45°;
(2)∵∠BAC=60°,
∴∠PMN=90°-$\frac{1}{2}×$60°=60°;
(3)∵∠BAC=α,
∴∠PMN=90°-$\frac{1}{2}$α.
点评 此题主要考查了等腰三角形的性质,直角三角形的性质,关键是掌握等腰三角形三线合一,在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.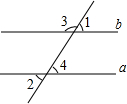 如图,不能确定直线a∥b的条件是( )
如图,不能确定直线a∥b的条件是( )
 如图,不能确定直线a∥b的条件是( )
如图,不能确定直线a∥b的条件是( )| A. | ∠1=∠2 | B. | ∠3+∠4=180° | C. | ∠2+∠3=180° | D. | ∠1+∠3=180° |
15.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-1=(x+1)(x-1) | C. | (x+1)(x+3)=x2+4x+3 | D. | x2+2x+1=x(x+2)+1 |
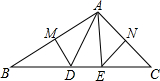 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,已知△ADE的周长为12cm,∠BAC=110°,求BC的长及∠DAE的度数.
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,已知△ADE的周长为12cm,∠BAC=110°,求BC的长及∠DAE的度数.