题目内容
13.观察下面一列数的规律并填空:1$\frac{1}{2}$,2$\frac{3}{4}$,3$\frac{5}{6}$,4$\frac{7}{8},5\frac{9}{10}$,…,则它的第10项是10$\frac{19}{20}$,第n个数是n$\frac{2n-1}{2n}$.(用含正整数n的式子表示)分析 首先根据这列数的前五个数分别是1$\frac{1}{2}$,2$\frac{3}{4}$,3$\frac{5}{6}$,4$\frac{7}{8},5\frac{9}{10}$,判断出这列数中每个数的整数部分、分数部分的变化规律;然后根据总结出的规律,判断出它的第10项的整数部分、分数部分各是多少,进而判断出它的第10项是多少;最后判断出第n个数的整数部分、分数部分各是多少,判断出这列数的第n个数是多少即可.
解答 解:∵这列数的前五个数的整数部分分别是1、2、3、4、5,
分数部分分别是$\frac{1}{2}=\frac{2×1-1}{2×1}$、$\frac{3}{4}=\frac{2×2-1}{2×2}$、$\frac{5}{6}=\frac{2×3-1}{2×3}$、$\frac{7}{8}=\frac{2×4-1}{2×4}$、$\frac{9}{10}=\frac{2×5-1}{2×5}$,
∴它的第10项的整数部分是10,分数部分是$\frac{2×10-1}{2×10}$=$\frac{19}{20}$,
∴它的第10项是10$\frac{19}{20}$,
∴这列数的第n个数是n$\frac{2n-1}{2n}$.
故答案为:10$\frac{19}{20}$,n$\frac{2n-1}{2n}$.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出这列数中每个数的整数部分、分数部分的变化规律.

练习册系列答案
相关题目
8.为了测试某种型号汽车的性能(车速不超过140km/h),对汽车的“刹车距离”进行测试,测试数据如下表:
(1)观察表格中的数据,估计刹车距离关于刹车时的车速的函数的类型,并确定一个满足这些数据的函数的表达式;
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
| 刹车时的车速x(km/h) | 0 | 10 | 20 | 40 | 60 |
| 刹车距离y(m) | 0 | 0.3 | 1.0 | 3.6 | 7.8 |
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
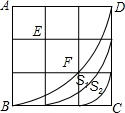 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.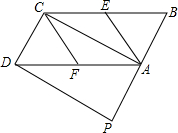 如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.
如图,在?ABCD中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DP∥AC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.